 |
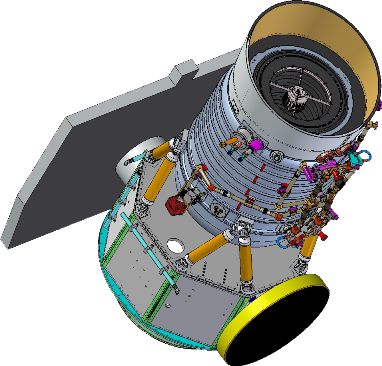
| Figure 1 - The WISE/NEOWISE flight system in its operational configuration. |



NEOWISE utilized the Wide-field Infrared Survey Explorer spacecraft in the same operational mode that was used for the original WISE mission. The WISE flight system and survey strategy are described by Wright et al. 2010, AJ, 140, 1868 and in section III of the All-Sky Release Explanatory Supplement. We provide a short summary of the WISE design and operations in this section to give context for the NEOWISE program.
The WISE/NEOWISE flight system, illustrated in Figure 1, consists of the spacecraft built by Ball Aerospace and Technologies Corp (now BAE Systems) and the payload built by the Space Dynamics Laboratory (SDL) at Utah State University.
The spacecraft design was based on the BATC RS300 single string spacecraft and provides full three-axis control. Primary attitude information is provided by two star trackers. Angular momentum is stored using four reaction wheels, and excess momentum is dumped using magnetic torquer rods. Flight system power is provided by a 20 amp-hour lithium-ion battery that is charged using a fixed 500-watt solar panel. Two omnidirectional S-band antennae receive commanding and transmit flight system telemetry. Payload science data are transmitted on the Ku-band via a fixed, high-gain antenna. All uplink and downlink transmission is done via the Tracking and Data Relay Satellite System (TDRSS).
 |
| Figure 1 - The WISE/NEOWISE flight system in its operational configuration. |
An exploded view of the WISE/NEOWISE payload is shown in Figure 2. The payload is a cryogenically cooled infrared instrument consisting of a 40-cm aperture telescope, scan mirror, and beam splitters to separate light into four bands. The entire optical assembly is housed within the two-stage solid-hydrogen cryostat. The 26.8-liter inner or primary hydrogen tank cools the two Si:As FPAs, while the 197-liter outer or secondary tank cools the rest of the optics to less than 17 K.
Light from the same sky field is measured simultaneously by WISE/NEOWISE using four focal plane array (FPA) detectors: two mid-wave infrared 4.2 and 5.4 μm cutoff HgCdTe arrays fabricated by Teledyne Imaging Sensors with 1024 x 1024 pixels, each 18 μm square, and two 1024x1024 pixel long-wave infrared (LWIR) Si:As BIB arrays from DRS Sensors & Targeting Systems with the same 1024 x 1024 pixel format and pitch. The first four and last four pixels in each row and column of the arrays are non-illuminated reference pixels and sensitive to only the DC bias. The active (photon-sensitive) area of the arrays is 1016 x 1016 pixels. The median pixel scale is 2.757"/pixel with a range of ±0.6% across both W1 and W2. The arrays image the same field of view simultaneously using three dichroic beam splitters. The measured performance of these detectors is summarized in Table 1, including updates inferred from on-orbit characterization of NEOWISE data following reactivation.
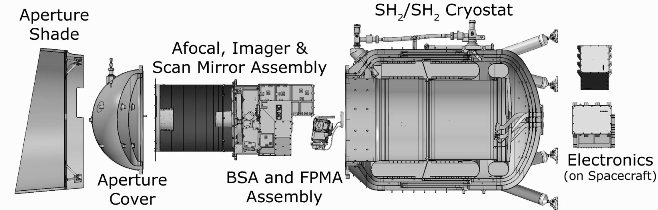 |
| Figure 2 - Exploded view of the WISE Payload. The aperture cover was ejected 15 days after launch. |
The arrays use sampling up the ramp (SUR). The 11 sec cadence between the individual exposures (frames) is divided into 10 intervals. A reset-read of the arrays occurs during the first 1.1 sec, followed by 8 read cycles each 1.1 sec apart and a final reset cycle while the scan mirror flays back (see I.2.b). For the W1 and W2 arrays, the 9 reads are multiplied by weights of 0, -7, -5, -3, -1, 1, 3, 5 and 7 and summed to give the slope of the ramp. The first sample showed excess noise during ground characterization and therefore was assigned a weight of zero, so the effective W1 and W2 exposure time is 7.7 sec. The read-out pattern for both arrays is shown in Figure 3. The reads occur simultaneously across 16 output channels following each 1.1 sec integration. This processing occurs in the payload Focal Plane Electronics Box (FEB) and the 8 individual non-destructive reads are sent to the Digital Electronics Box for the slope-computation and saturated/broken-pixel tagging (see below). Note that the orientation of the layout in Figure 3 on the sky (as represented in the Single-exposure images) is different for W1 and W2. For the W1 single-exposures, pixel 1,1 (bottom-left-most pixel) corresponds to pixel position 1,1024 in Figure 3, while for W2, pixel 1,1 is located at position 1,1 in the Figure. This is helpful in determining why some fast-moving objects (including artificial satellites) have truncated streaks in some of the single-exposures.
The dynamic range (after A/D conversion) in the FEB is 0 to 214 - 1 (= 16,383 DN) while in the DEB (the outputs that are downlinked) it's 0 to 215 - 1 (= 32,767 DN). However, the maximum of the DEB range for storing photo-electron counts is actually 32,752 DN. The higher values are reserved to tag saturated and broken pixels. The saturated pixels are assigned values of 32,753 to 32,761, corresponding accordingly to the sample read where it first saturated in the ramp, with 32,761 implying it saturated on sample #9. Broken pixels (or more precisely pixels with negative slopes) are assigned 32,767. For details on how this information is propagated to the single-exposure image masks, see section IV.2.a.iii.
To compensate for the higher focal plane temperatures at the start of Reactivation survey operations, the saturation threshold values used to encode saturated pixels in DEB processing were adjusted to lower values than were use during the primary WISE mission phases (Reactivation: 14,300DN (W1) and 11,400DN (W2) compared to WISE Primary 16,000DN (W1) and 14,500DN (W2)). These saturation thresholds were held during the Reactivation survey with the exception of an ~8.2 day interval in July of 2024. The DEB saturation threshold values were inadvertently reset to the higher values used during the primary WISE mission when the survey observations were resumed on 13 July 2024 UTC following a short standby mode. The DEB saturation thresholds were reset to the correct Reactivation survey values on 24 July 2024 UTC. During the time when the incorrect saturation thresholds were being used, saturated pixels may not have been correctly flagged in the DEB processing, and therefore may not have been flagged in the bit masks generated during NEOWISE processing (IV.2.a.ii) and properly handled during downstream source extractions.
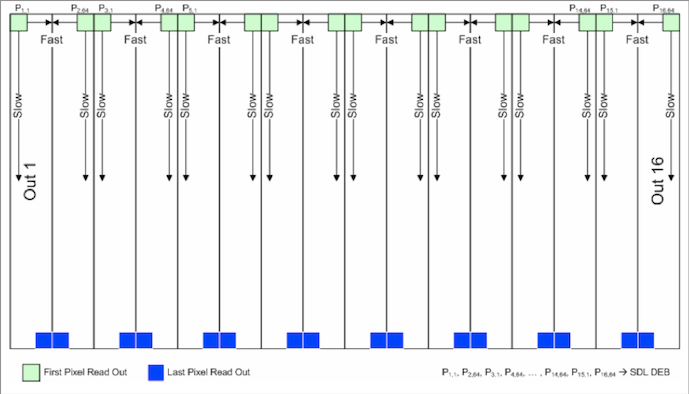 |
| Figure 3 - Pixel readout order for the HgCdTe (W1 and W2) detectors showing the 16 output channels. |
| Parameter | W1 Performance/value | W2 Performance/value |
| Wavelength Range[1] (µm) | 2.8-3.8 | 4.1-5.2 |
| Effective (Isophotal) Wavelength[1] (µm) | 3.35 | 4.60 |
| Operating Temperature Range[2] (K) | 31 ~ 75.5 | 31 ~ 75.5 |
| Array Format (pixels) | 10242 (10162 active) | 10242 (10162 active) |
| Quantum Efficiency[3] (mean over band, with AR coating) (%) | >70 | >70 |
| Pixel Pitch (µm) | 18 | 18 |
| Pixel Operability | >90% | >90% |
| Dark Current[3] (mean, @ operating temperature) (e-/sec) | <1 | <1 |
| Electronic Gain from DEB output[4] (e-/DN) | 2.9 | 3.4 |
| Read Noise from DEB output[4] (e-, SUR-slope rms) | 7.11 | 9.52 |
| Read Noise from FEB[3] (e-, CDS rms) | ~ 19 | ~ 19 |
| Well Capacity (e-) | >100,000 | >100,000 |
| Power Dissipation (mW) | 6.7 | 6.7 |
| #Output Channels | 16 | 16 |
The temperature of the payload's beamsplitter mount assembly, which is a proxy for the HgCdTe detector focal plane temperature, is plotted as a function of time from the beginning of the original cryogenic WISE mission until February 2015 of the NEOWISE Reactivation mission in Figure 4. While the inner and outer cryogenic tanks held hydrogen ice, the Si:As arrays operated at 7.8 K, and the HgCdTe arrays were operated at 32 K. Following the exhaustion of cryogens in both tanks in September 2010, the telescope and FPAs warmed until reaching radiative equilibrium with the sky at a temperature of approximately 74K. The relatively wide range of operating temperatures for the HgCdTe detectors allowed WISE (and then NEOWISE) to continue surveying at sensitivities close to those achieved during the cryogenic mission phase (II.1.c.iii). The Si:As detectors are saturated by the flight system thermal emission at these temperatures, and no useful W3 or W4 data are collected.
WISE was placed into hibernation in February 2011, and during that time the telescope was pointed constantly near the north ecliptic pole and viewed the Earth for half of its orbit. The focal planes warmed to over 200 K as a result. The variations in temperature from February 2011 to October 2013 are due to seasonal changes in the Earth heating of the flight system shell. Once the spacecraft was restored to zenith pointing for NEOWISE in October 2013, the temperatures cooled passively back to <76K within about three months.
The focal plane temperature trend since the start of the NEOWISE survey is shown in Figure 11. Temperatures undergo annual variations with peaks shortly after the summer and winter solstices, and minima following the equinoxes. These seasonal variations are superimposed on a systematic rise over time that corresponds to the increase in heating by the Earth as the orbit drifts off the terminator.
The delivered NEOWISE Point Spread Functions (PSFs) are described in section IV.2.b.i. Profiles through the major and minor axes of the PSFs are illustrated in Figure 5. The FWHM of the major axes of the PSFs is 6.4 and 6.7 arcsec in W1 and W2, respectively. The NEOWISE W1 PSFs are slightly more elongated than during the original WISE mission.
The WISE filter bandpasses and photometric system are described in section IV.4.h.v of the All-Sky Release Explanatory Supplement. The relative spectral response functions profiles of the bandpasses are shown below in Figure 6.
NEOWISE surveys using a freeze-frame scanning technique similar to those used by 2MASS and the Spitzer MIPS instrument. The telescope scans the sky between the ecliptic poles in great (semi-)circles approximately perpendicular to the Earth-Sun line. As the telescope boresight scans continuously, an articulated scan mirror within the Payload freezes the motion of the sky on the focal plane detectors while a Single-exposure is acquired by each of the four arrays. The scan mirror flies back to acquire the next sky position and a new exposure cycle begins every 11 seconds. The line-of-sight advances 42' per exposure, resulting in ~10% overlap between adjacent exposures.
The detectors are read out non-destructively nine times with 1.1 second spacing for each Single-exposure. A single value for the fitted sample-up-the-ramp slope is computed on board for all pixels, and eventually downlinked as the Single-exposure. The first readout of the HgCdTe W1 and W2 detectors is discarded, so their effective exposure time is 7.7 seconds.
The NEOWISE orbital scan precession produces approximately 90% overlap in the ecliptic longitude direction between scans that are adjacent on the sky. As discussed below, longitudes between subsequent scans are toggled forward and back slightly to smooth coverage variation due to the South Atlantic Anomaly (SAA), and are adjusted by approximately 10° biweekly to avoid the moon (see also III.4.b in the All-Sky Release Supplement for details of these maneuvers). The ecliptic longitude of WISE scan semi-circles is shown as a function of scan number (time) in Figure 7.
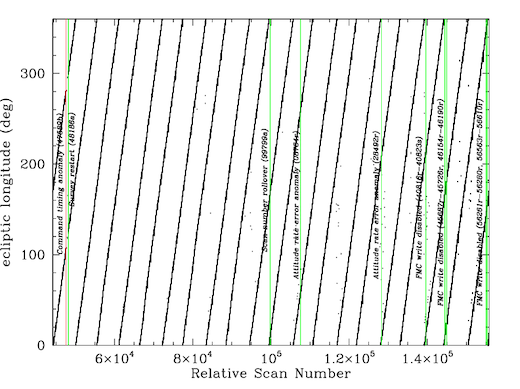 |
| Figure 7 - Ecliptic longitude of the scan semi-circles as a function of scan number during the NEOWISE Reactivation mission, 13 December 2013 to 1 August 2024 UTC. Survey observations were halted for 19 days in April 2014 during a safe hold following a command timing anomaly. Brief interruptions due to attitude rate anomalies occurred in August 2019 and June 2021. Small gaps in survey data coverage due to inadequate TDRSS downlink pass time availability occurred in July and December 2022, November and December 2023, and May and June 2024. |
NEOWISE scans are offset slightly from the perpendicular to the Sun line by a variable amount that is controlled by the settings for the following configurable survey parameters:
During the original (2010-2011) WISE/NEOWISE mission, these parameters resulted in a small (~2.5 deg) offset of the line-of-sight from the perpendicular to the Sun line. Since that time, the NEOWISE orbit precession rate has drifted from its ideal Sun-synchronous value due to a decrease in altitude caused by the atmospheric drag in low-Earth orbit. The altitude cannot be corrected because NEOWISE does not have a propulsion system. To compensate for the orbit drift, some of the survey parameters were modified in January 2015, January 2016, March 2017 and January 2018 to optimize telescope pointing relative to both the Sun and Earth, as indicated in Table 2. Specifically, for each year of NEOWISE Reactivation, survey parameters are changed so that scans are made near the zenith as of summer solstice on the 6PM side of the orbit, and perpendicular to the Sun on the 6AM side. No changes were made to the survey parameters after 2018.
Table 2 provides the values of these parameters during the original WISE/NEOWISE mission in 2010-2011, and during the NEOWISE Reactivation mission. The changing orbit orientation and the updated survey pointing strategy to address the orbit changes are illustrated in Figure 8.
| Survey Parameter | 2010-2011 | 2013-2014 | 2015 | 2016 | 2017 | 2018-2024 |
|---|---|---|---|---|---|---|
| TOGGLE (deg) | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 |
| MOONAVOID (deg) | 1.23-1.38 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 |
| DIHEDRAL (deg) | 2.5 | 2.5 | 4.13 | 7.0 | 9.0 | 11.0 |
| ECLIPSEBIAS (deg) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| BIAS (deg) | 2.5 | 0.0 | 4.13 | 7.0 | 9.0 | 11.0 |
| MINMOON (deg) | 5.0 | 5.0 | 5.0 | 3.0-5.0 | 3.0-5.0 | 3.0-5.0 |
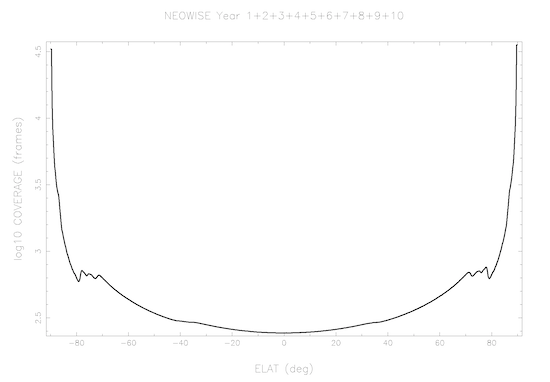
The in-scan (ecliptic latitude) and cross-scan (ecliptic longitude) overlaps build up multiple independent exposures on each point of the sky over the course of the survey. NEOWISE scanned the sky nearly eighteen complete times during the first 10 years of operations, with each sky coverage epoch separated by approximately six months. Figure 9 illustrates the Single-exposure depth-of-coverage in the first ten years. A total of 20,349,725 Single-exposures were acquired during this time.
Twelve independent exposures are made on each sky point near the ecliptic plane during each survey sky pass, and the number of samples increases towards the ecliptic poles (Figure 10). The combined ten-year NEOWISE data set typically contains ~220 independent measurements of objects near the ecliptic plane, and over 34,000 measurements very close to the ecliptic poles.
Survey observations were interrupted on April 4, 2014 because of a safe hold that followed an anomalous command timing slip. The flight system was kept in safe mode for 19 days while the cause of the anomaly was investigated. Survey observations resumed on April 23 at the ecliptic longitudes that normally would have been scanned in the absence of the safe-hold event. This resulted in approximately 10% of the sky in the ecliptic longitude ranges 107.5°<λ<126.1° and 281.4°<λ<299.2° not being surveyed during the first sky coverage epoch. These regions were surveyed normally during subsequent epoch sky coverages, but show up as the two bands of lower depth-of-coverage in Figure 9. Data acquisition was also interrupted for 13 hours on August 21, 2019 and 21 hours on June 29, 2021 due to attitude rate anomalies. The coverage loss due to those interruptions was small and not apparent in Figure 9.
Additional small gaps in sky coverage resulted when science image data writing to the on-board storage was interrupted in the fourth, ninth, tenth, and eleventh survey years, as discussed in I.2.c.vi.,
 |
| Figure 10 - Aziumathally-averaged Single-exposure depth-of-coverage plotted as a function of ecliptic latitude, for the full NEOWISE Reactivation mission. |
Key events during the NEOWISE Reactivation survey are listed in Table 3. These include major survey milestones, such as survey start and end, sky coverage completions, and dates and times of significant interruptions to survey operations. A more detailed timeline of both survey and data processing for the original WISE mission and the NEOWISE Reactivation Survey is provided in Table 4.
| Date | UTC | Scan Number | Event |
|---|---|---|---|
| 2013-08-29 | NEOWISE Reactivation project start | ||
| 2013-10-03 | 15:13:00 | Command to zenith pointing (cooldown begins) | |
| 2013-12-05 | 19:26:50 | 43969b | First engineering sky data collected. |
| 2013-12-13 | 18:39:35 | 44212a | NEOWISE survey operation start |
| 2014-04-04 | 01:32:50 | 47589b | Command timing anomaly. Survey observations halted. |
| 2014-04-16 | 18:23:15 | 47977a-47977b | Test survey scans. |
| 2014-04-17 | 16:52:57 | 48005a-48005b | Test survey scans. |
| 2014-04-17 | 19:01:40 | 48008a-48008b | Test survey scans. |
| 2014-04-17 | 22:07:47 | 48012a-48012b | Test survey scans. |
| 2014-04-23 | 16:40:44 | 48186a | Survey observations resume |
| 2014-06-16 | First inertial sky coverage epoch complete | ||
| 2014-07-17 | 15:40:59 | 50769a | Star tracker thermal set points updated |
| 2014-09-29 | 16:40:08 | 53021a | Survey observations halted. Flight software reset. |
| 2014-09-30 | 01:17:46 | 53032a | Survey observations resume |
| 2014-10-09 | 15:54:04 | 53324a | Survey observations halted. Flight software reset. |
| 2014-10-09 | 19:40:02 | 53329a | Survey observations resume |
| 2014-12-13 | Second inertial sky coverage epoch complete | ||
| 2014-12-13 | 07:26:42 | 55289b | Final NEOWISE Year 1 scan |
| 2014-12-13 | 07:27:49 | 55290a | First NEOWISE Year 2 scan |
| 2015-01-08 | 12:46:39 | 56089a | Survey parameter updates begin |
| 2015-02-05 | 12:28:27 | 56941a | Survey parameter updates complete |
| 2015-06-16 | Third inertial sky coverage epoch complete | ||
| 2015-06-23 | 11:29:36 | 61144a | Leap second error corrected |
| 2015-12-13 | Fourth inertial sky coverage epoch complete | ||
| 2015-12-13 | 10:47:22 | 66418a | Final NEOWISE Year 2 scan |
| 2015-12-13 | 11:26:48 | 66418b | First NEOWISE Year 3 scan |
| 2016-01-21 | 12:00:00 | 67609a | Survey parameter updates begin |
| 2016-02-04 | 12:00:00 | 68036a | Survey parameter updates complete |
| 2016-03-21 | 20:37 | 69438a | Byte-shift anomaly. Intermittent data loss. |
| 2016-03-23 | 16:30 | 69505b | Byte-shift corrected. |
| 2016-06-14 | 72041b | Fifth inertial sky coverage epoch complete | |
| 2016-12-10 | 77501b | Sixth inertial sky coverage epoch complete | |
| 2016-12-13 | 12:00:01 | 77590a | Final NEOWISE Year 3 scan |
| 2016-12-13 | 12:02:46 | 77590b | First NEOWISE Year 4 scan |
| 2017-02-27 | 12:56 | 79912a | Payload Flash Memory Card disabled |
| 2017-02-27 | 16:12:12 | 79917a | Payload Flash Memory Card re-enabled |
| 2017-03-06 | 00:00:00 | 80110a | Survey parameter updates begin |
| 2017-03-19 | 00:00:00 | 80506a | Survey parameter updates complete |
| 2017-06-13 | 83161b | Seventh inertial sky coverage epoch complete | |
| 2017-12-09 | 88625b | Eighth inertial sky coverage epoch complete | |
| 2017-12-13 | 07:08:38 | 88733a | Final NEOWISE Year 4 scan |
| 2017-12-13 | 07:11:56 | 88734a | First NEOWISE Year 5 scan |
| 2018-01-11 | 12:00:00 | 89626a | Survey parameter updates begin |
| 2018-01-25 | 12:00:00 | 90054a | Survey parameter updates complete |
| 2018-06-16 | 94378a | Ninth inertial sky coverage epoch complete | |
| 2018-12-10 | 09:23:53 | 99799a | Final scan with original scan_id definition |
| 2018-12-10 | 09:28:28 | 01000r | First scan with new scan_id definition |
| 2018-12-11 | 01042r | Tenth inertial sky coverage epoch complete | |
| 2018-12-13 | 08:00:01 | 01089r | Final NEOWISE Year 5 scan |
| 2018-12-13 | 08:04:26 | 01090r | First NEOWISE Year 6 scan |
| 2019-06-15 | 06710r | Eleventh inertial sky coverage epoch complete | |
| 2019-08-21 | 09:01:19 | 08764r | Attitude rate error fault. Flight system in standby mode. |
| 2019-08-21 | 22:39:22 | 08782r | Survey operations resume. |
| 2019-12-11 | 12178r | Twelfth inertial sky coverage epoch complete | |
| 2019-12-13 | 11:50:35 | 12253r | Final NEOWISE Year 6 scan |
| 2019-12-13 | 12:10:34 | 12254r | First NEOWISE Year 7 scan |
| 2020-06-13 | 17826r | Thirteenth inertial sky coverage epoch complete | |
| 2020-12-12 | 23402r | Fourteenth inertial sky coverage epoch complete | |
| 2020-12-13 | 11:53:34 | 23446r | Final NEOWISE Year 7 scan |
| 2020-12-13 | 11:57:58 | 23447r | First NEOWISE Year 8 scan |
| 2021-06-15 | 29078r | Fifteenth inertial sky coverage epoch complete | |
| 2021-06-29 | 02:29:15 | 29492r | Attitude rate error fault. Flight system in standby mode. |
| 2021-06-29 | 23:47:50 | 29519r | Survey operations resume. |
| 2021-12-11 | 34546r | Sixteenth inertial sky coverage epoch complete | |
| 2021-12-13 | 01:11:06 | 34601r | Final NEOWISE Year 8 scan |
| 2021-12-13 | 01:14:13 | 34601s | First NEOWISE Year 9 scan |
| 2022-06-14 | 40226r | Seventeenth inertial sky coverage epoch complete | |
| 2022-07-03 | 22:25 | 40816r | Survey data writing to Flash Memory suspended |
| 2022-07-04 | 04:10 | 40823s | Survey data writing to Flash Memory resumed |
| 2022-12-09 | 17:04 | 45687r | Survey data writing to Flash Memory suspended |
| 2022-12-10 | Eighteenth inertial sky coverage epoch complete | ||
| 2022-12-10 | 23:27 | 45726r | Survey data writing to Flash Memory resumed |
| 2022-12-13 | 12:11:43 | 45803r | Final NEOWISE Year 9 scan |
| 2022-12-13 | 12:39:57 | 45804r | First NEOWISE Year 10 scan |
| 2022-12-24 | 22:05 | 46154r | Survey data writing to Flash Memory suspended |
| 2022-12-26 | 02:15 | 46190r | Survey data writing to Flash Memory resumed |
| 2023-06-16 | 51502r | Nineteenth inertial sky coverage epoch complete | |
| 2023-11-17 | 22:12 | 56261r | Survey data writing to Flash Memory suspended |
| 2023-11-18 | 12:30 | 56280r | Survey data writing to Flash Memory resumed |
| 2023-11-27 | 16:10 | 56563r | Survey data writing to Flash Memory suspended |
| 2023-11-29 | 04:16 | 56610r | Survey data writing to Flash Memory resumed |
| 2023-12-12 | 57026r | Twentieth inertial sky coverage epoch complete | |
| 2023-12-13 | 02:53:18 | 57041r | Final NEOWISE Year 10 scan |
| 2023-12-13 | 02:57:42 | 57042r | First NEOWISE Year 11 scan |
| 2024-05-31 | 12:52 | 62338r | Survey data writing to Flash Memory suspended |
| 2024-06-03 | 09:00 | 62427r | Survey data writing to Flash Memory resumed |
| 2024-06-07 | 12:04 | 62556r | Survey data writing to Flash Memory suspended |
| 2024-06-10 | 00:14 | 62635r | Survey data writing to Flash Memory resumed |
| 2024-06-14 | 62790r | Twenty-first inertial sky coverage epoch complete | |
| 2024-07-12 | 16:56:08 | 63658r | Attitude rate error fault. Flight system in standby mode. |
| 2024-07-13 | 21:51:41 | 63696r | Survey operations resume. DEB saturation thresholds inadvertently set to WISE Primary survey values. |
| 2024-07-24 | 03:24:12 | 64017r | DEB saturation thresholds reset to Reactivation survey values. |
| 2024-08-01 | 06:59:48 | 64272r | Final NEOWISE Reactivation exposure. End of survey operations |
| 2024-08-08 | 22:21:13 | NEOWISE flight system deactivated. | |
| 2024-11-02 | 00:49 | WISE/NEOWISE re-enters the Earth's atmosphere. | |
The WISE flight system was placed into hibernation in February 2011 after completing its primary mission. At that time, the payload was powered off, as were most spacecraft components. During hibernation, the flight system was held in an inertial pointing configuration, with solar panels oriented toward the Sun and the telescope bore sight pointed near the north ecliptic pole. This resulted in the Earth being viewed for approximately half of each orbit. This resulted in the focal planes warming to approximately 200 K (Figure 4), with seasonal variations caused by changing exposure to the Earth.
Exploratory S-band contacts were made with WISE on September 9 and November 28 of 2012 to poll the status of the flight system. All systems appeared nominal during those contacts.
The NEOWISE program had its official start on August 29, 2013. S-band contacts were re-established with the flight system on September 25, 2013, and power was restored to some of the spacecraft components including the star trackers. NEOWISE was commanded to "point-standby" mode on October 3, 2013, which restored near-zenith pointing. The focal plane temperature was 202 K at this point, but began cooling quickly when exposure to the Earth was halted. The temperature had cooled to ~77 K by December 5, 2013, when the detectors were powered on and one test survey scan was acquired. The payload was powered on and scanning restarted on December 5, 2013, and the first engineering scanning data were collected. All flight system performance was nominal at this point, and the imaging data were nominal, albeit with the higher dark currents expected for the warm temperatures.
NEOWISE survey observations began at 18:39:35 on December 13, 2013 UTC. The focal plane temperature at that point was 75.7 K, and still cooling rapidly as can be seen in Figure 11 which shows payload component temperatures during the first 10 years of NEOWISE survey operations. The beamsplitter mount assembly (BSA Mount) is the closest proxy to the focal plane temperature, although all of the components follow the same trends.
The temperature profile in Figure 11 shows a number of features. At the start of the survey, temperatures were still cooling, not having quite reached radiative equilibrium. The abrupt drop in temperature on April 4, 2014 occurred when the payload was powered off following the ADCS commanding anomaly, which is described below. This allowed the focal planes to cool to ~72 K when they were powered back on for the resumption of survey observations on April 23, 2014.
The general temperature behavior exhibits regular seasonal variations with minima in March and November that follow the equinoxes when exposure to Earth heating of the telescope shell is at a minimum. There are broad temperature maxima in July and January following the summer and winter solstices, respectively, when heating is near its peak. The slow, systematic temperature increase with time during the first 6-7 years of the survey occurred because of the drift of the NEOWISE orbit off the terminator and subsequent increase in heating from the Earth. After 2016, the drift of the WISE orbit slowed and then reversed in 2021 due to a decreasing torque from the Moon (Fig. 12). The reversal led to the decrease in payload temperature in 2021 and 2022. The increased orbital decay rate during the solar maximum starting in 2023 caused the angle away from the terminator to increase again, and thus the payload temperatures began to increase dramatically in 2024.Figure 13 illustrates the altitude of the spacecraft during the WISE primary and NEOWISE Reactivation mission. The altitude remained relatively stable near ~500km through most of the Reactivation survey until mid-2022 when the increase in solar activity led to increased atmospheric drag and accelerated descent of the spacecraft. Survey operations were halted at the end of July 2024 when the altitude reached approximately 400 km. The spacecraft was decommissioned on August 8, 2024. The altitude continued to decrease following decommissioning and the WISE/NEOWISE spacecraft re-entered the Earth's atmosphere on November 2, 2024 UTC.
NEOWISE survey images are tagged with a UTC time that is computed during the INGEST data processing step by converting the spacecraft clock time using the SPICE Spacecraft Clock Kernel (SCLK) and Leap Second Kernel (LSK) provided by the Mission Operations team. The UTC times assigned to the images differ slightly from true UTC because of several effects that are described below. The corresponding times associated with source detections made on the images, including solar system object detections reported to the MPC, will have the same small systematic and random offsets with respect to UTC.
Exposure Time Offset - The conversion of spacecraft clock time to UTC was designed at the start of the original WISE cryogenic mission to correspond the midpoint of the 12 μm (W3) band exposure because most asteroid detections during the full cryogenic phase were made in that band. The midpoint of the exposure was defined as the time at which the track followed by the telescope boresight crossed the middle line of the W3 detector during one 8.8 sec freeze-frame scanning exposure. During the NEOWISE Post-Cryo and Reactivation missions, most asteroid detections are made in the 4.6 μm (W2) band. Because the first non-destructive reads of the W2 (and W1) detectors are discarded, the effective exposure times are 7.7 sec, and their mid-points occur 0.57 sec later than the W3 (and W4) exposures. Therefore, the UTC observation times assigned to all images and corresponding source detections during the NEOWISE Post-Cryo and Reactivation phases are actually 0.57 sec earlier than the actual UTC of the mid-points of the observations.
Leap Second Error - While preparing for the use of the June 30, 2015 leap second, it was found that the NEOWISE spacecraft-to-UTC time conversions were made using an out-of-date Leap Second Kernel that did not include the June 2012 leap second that took place while the WISE/NEOWISE spacecraft was in hibernation. This resulted in time assignments that lagged UTC time by one second. For example, for an observation on day 100 of 2014 at 00:00:00.2 UTC (2014-100T00:00:00.2), the UTC timestamp assigned to the images and source detections would have been 2014-099T23:59:59.2. This error was corrected on June 23, 2015 at 11:29:30.47 UTC. The one-second offset from UTC is present in all observations from the start of the NEOWISE Reactivated mission on December 13, 2013 until the time of that correction. The first corrected tracklet time stamp reported to the MPC was 2015 06 23.48882, for the Main Belt Asteroid 32154 (2000 MH), with the NEOWISE tracklet label N0080fi.
Spacecraft Clock Rate Drifts - The rate of the WISE/NEOWISE on-board spacecraft clock drifts slightly in response to temperature variations in the spacecraft bus. Depending on the temperature trends, the sign of the drift may be positive or negative. Corrections are made for the drift routinely during the survey, such that the absolute value of the accumulated drift relative to UTC remains below 0.6 sec. There was a brief interval between April 9, 2017 22:49:53 UTC and April 11, 2017 00:00:00 UTC when the drift offset exceeded 0.6 sec, reaching a maximum of 0.75 sec. The overall time-average uncertainty from this effect is on the order of 0.25 sec or less, with a zero net mean.
A NEOWISE scan refers to the observations or block of survey imaging data acquired between two flight system maneuvers, such as reorientation of the instrument boresight near the ecliptic poles, or slews to acquire TDRSS for data downlink contacts. Because maneuvers often took place near the ecliptic poles, a scan is associated with the image data from approximately a half-orbit. However, scans can cover less or more than half of the arc between ecliptic poles.
Scans are identified in the various NEOWISE data and metadata by the scan_id. The scan_id was defined at the beginning of the cryogenic WISE mission as a six-character string having the general form SSSSSx. For data taken by WISE/NEOWISE up through 12/10/2018, the two parts of the scan_id are defined as follows:
For example, the first scan of the NEOWISE Reactivation survey is 44212a. This was the first scan after the NEP crossing in the 22,106th WISE/NEOWISE orbit.
The WISE/NEOWISE spacecraft executed its 50,000th orbit on 12/16/2018. At this point, the numerical portion of the scan_id (SSSSS) would have changed from 99999 to 100000, exceeding the five digits allocated in the scan_id string. To avoid considerable modifications to the NEOWISE data processing and archiving system that would be required to change the format of the scan identifier to seven characters, the six-character scan_id format was preserved and the definition was modified as follows:
The final scan having the original scan_id definition is 99799a executed on 12/10/2018 UTC. The scan immediately following has scan_id 01000r. The final NEOWISE Reactivation mission scan is 64272r. This was the first scan following the NEP crossing in the 81,536th WISE/NEOWISE orbit.
NEOWISE achieved an observation efficiency of >92% over the full life of the the Reactivation mission. This efficiency is estimated by dividing the total number of exposures that were acquired and downlinked, by the theoretical maximum number of exposures made between the start and end date of survey operations, assuming an 11 sec duty cycle per exposure. This estimate takes into account the available survey time lost to planned survey interruptions to downlink science data and engineering telemetry. It does not take into account survey time lost due to positioning slews between scans or a number of other unplanned survey interruptions. Some of the unplanned survey interruptions are described below.
During regular NEOWISE survey operations, survey data acquisition was interrupted on average three times per day to downlink science data and engineering telemetry via High-Rate Ku-band transmitted from the flight system to TDRS for relay to the TDRSS terminal at White Sands Complex (WSC). During each downlink contact, the flight system was body-pointed to orient the high gain Ku-band antenna towards a TDRS element. Downlink contacts were made preferentially during scans when WISE approached within 45° of the Ecliptic poles so that survey outages took place where the nominal depth-of-coverage was highest.
Approximately 60 minutes per day were used during regular survey operations for downlink contacts. This included approximately 40 minutes for data transfer time and 20 minutes for slewing to body point the high gain antenna towards a TDRS element. The actual downlink contact time each day varied depending on TDRSS availability and viewing geometry between the flight system and the TDRS elements.
An accumulation of command timing slips resulted in a brief loss of NEOWISE attitude control on April 3, 2014. Control was restored quickly and the flight system was placed into a safe hold while the problem was diagnosed. Survey observations were halted and the payload was powered off during the safe hold.
The command timing slips were caused when an interrupt generated to mark a tick of the spacecraft clock was ignored when another interrupt clashed with it. This resulted in a missed execution of the 100 Hz real-time flight software. If three such timing slips accumulated, attitude control would be lost. This had not occurred before in the original WISE mission, or earlier in the NEOWISE Reactivation survey.
The safe hold was maintained for 19 days while the problem was diagnosed and mitigations were planned. Several test survey scans were executed during the safe hold to monitor payload health (see Table 3). The payload performance was nominal in these scans, and data from them are included in the NEOWISE Release. The focal plane temperatures during these test scans will likely be the lowest of any taken during the NEOWISE Reactivation survey.
Command timing slips occurred twice more during the first year of NEOWISE reactivation, in September and October 2014. To avoid loss of attitude control, the spacecraft flight software was reset preemptively after two timing slips were diagnosed. This led to only brief interruptions in the surveying, as noted in Table 3. A procedure to correct the timing slips that did not require resetting software and did not interrupt survey observations was developed in late 2014. This procedure was used successfully twice during 2015, and as a result, there were no interruptions to normal survey operations during the second year.
The April command timing anomaly and safe hold resulted in approximately 10% of the sky in the ecliptic longitude range 107.5°<λ<126.1° and 281.4°<λ<299.3° not being covered during the first inertial sky pass. These regions were surveyed during each of the later sky passes.
A small amount of raw survey image data were lost in March 2016 due to an anomaly in the payload electronics that introduced a 5-byte shift in the downlinked science data packets. The anomaly occurred on 21 March 2016 and was corrected by resetting the electronics (FIFO) on 23 March. Because the nature of the anomaly was recognized early, much of the affected data could be corrected on the ground. Data loss was limited to the relatively small number of framesets that are summarized in Table 5.
| Date | Scan Number | Frame(set) | Description |
|---|---|---|---|
| 2016-03-21 | 69450a | 010 | W1 frame missing |
| 2016-03-22 | 69460a | 131 | W2 frame missing |
| 2016-03-22 | 69474a | 022 | W2 frame missing |
| 2016-03-22 | 69474a | >022 | W1,W2 frames missing |
| 2016-03-22 | 69476a | 001-062 | W1,W2 frames missing |
| 2016-03-22 | 69476a | 063 | W1 frame missing |
| 2016-03-23 | 69488a | 073 | W1 frame missing |
| 2016-03-23 | 69505b | 198 | W2 frame missing |
| 2016-03-23 | 69505b | 199-216 | W1,W2 frames missing |
| 2016-03-23 | 69505b | 217 | W2 frame missing |
During normal survey operations, the NEOWISE focal plane detectors are read out continuously. The survey imaging data are normally written to the payload's Flash Memory Card (FMC), except when the survey pattern is interrupted while the spacecraft is re-oriented to enable data downlink to TDRSS. Survey data writing to the FMC is resumed when survey scanning resumes following the downlink contact pass.
There were several instances when survey data writing to the FMC was interrupted outside of the regular downlink pass times, while the spacecraft performed regular survey observations. These interruptions resulted in the loss of survey imaging data, and if the duration of the interruptions was long enough, this also resulted in loss of coverage of the fixed sky.
Table 6 contains a listing of the FMC write interruptions during NEOWISE survey observation. For each event, the times and identifications of the final survey exposure before the write interruption and the first survey exposure following the write resumption. The mean center ecliptic longitudes of the scans that bound the interruptions are also given. Pairs of longitudes are given for each to cover the two sides of the orbits on the sky. If the gap between bounding longitudes exceeds the 47 arcmin width of the NEOWISE focal plan detectors, then there will be a loss of survey coverage of the fixed sky for that sky coverage pass. The approximate percentage of sky coverage loss is given in column 11 of Table 6.
The first FMC write interruption occurred on 27 February 2017 because the FMC was inadvertently disabled. The FMC was re-enabled after approximately 3.5 hours and data recording resumed. There was no net loss in sky coverage.
Writing payload image data to the FMC was intentionally suspended seven times during the 9th, 10th, and 11th survey years to avoid filling the available payload memory. Leading up to these interruptions, downlink pass time opportunities were significantly decreased because of TDRSS failures of TDS and SA1, the loss of the Guam TDRS ground station, and because pass time had been allocated to higher priority users. The duration of five of these events were long enough to result in fixed sky coverage losses.
| Final Exposure Before FMC Write Suspended | First Exposure after FMC Write Resumed | Sky Coverage Loss | Cause | UT Date | UTC | Scan ID | Frameset | Ecliptic Longitudes (boresight) | UT Date | UTC | Scan ID | Frameset | Ecliptic Longitudes (boresight) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2017-02-27 | 12:44:37 | 79912a | 173 | 83.8/248.0 | 2017-02-27 | 16:12:12 | 79917a | 173 | 83.6/248.3 | 0% | Inadvertant command error |
| 2022-07-03 | 22:24:54 | 40816r | 142 | 11.1/214.9 | 2022-07-04 | 04:17:20 | 40823r | 001 | 11.4/214.8 | 0% | Lack of TDRSS downlink pass opportunities |
| 2022-12-09 | 17:04:27 | 45687r | 038 | 8.7/168.4 | 2022-12-10 | 23:27:29 | 45726r | 001 | 9.7/169.5 | 0.2% | Lack of TDRSS downlink pass opportunities |
| 2022-12-24 | 22:04:52 | 46154r | 016 | 25.6/182.4 | 2022-12-26 | 02:15:19 | 46190r | 001 | 26.8/183.4 | 0.2% | Lack of TDRSS downlink pass opportunities |
| 2023-11-17 | 22:11:59 | 56261r | 230 | 144.8/348.2 | 2023-11-18 | 12:29:35 | 56280r | 001 | 145.2/348.5 | 0% | Lack of TDRSS downlink pass opportunities |
| 2023-11-27 | 16:10:33 | 56563r | 179 | 155.8/356.1 | 2023-11-29 | 04:16:28 | 56610r | 002 | 157.2/357.4 | 0.3% | Lack of TDRSS downlink pass opportunities |
| 2024-05-31 | 12:52:21 | 62338r | 260 | 182.2/338.9 | 2024-06-03 | 08:59:57 | 62427r | 179 | 185.0/341.6 | 1.1% | Lack of TDRSS downlink pass opportunities |
| 2024-06-07 | 12:04:09 | 62556r | 147 | 189.8/346.4 | 2024-06-10 | 00:14:49 | 62635r | 001 | 192.1/348.7 | 0.9% | Lack of TDRSS downlink pass opportunities |
NEOWISE tripped attitude rate error faults on August 21, 2019, June 26, 2021, and July 12, 2024 that resulted in the flight system entering Standby mode. Survey operations were resumed approximately 13.5 hours, 23.3 hours, and 28.9 after the 2019, 2021, and 2024 faults occurred, respectively. Analysis of the spacecraft attitude control system performance just prior to the rate error suggests that NEOWISE may have been struck by debris leading to the anomalous motion in each case.
In August 2019, the survey interruption occurred during scan 08764r centered along ecliptic longitude of λ=58.92°. The last complete scan prior to that was 08763r centered on λ=259.51°. Observations resumed with scan 08782r at longitude λ=59.85°, followed by scan 08783r at λ=260.21°. Because of the width of the NEOWISE focal plane, the survey interruption resulted in a coverage gap of ~0.34° wide on the ecliptic plan, centered near λ=59.5°. There was no gap on the opposite side of the sky, only reduced depth-of-coverage centered on λ=259.86°.
In June 2021, the attitude rate fault occurred during scan 29492r centered along ecliptic longitude of λ=8.38°. The last complete scan prior to that was 29491r centered on λ=208.98°. Observations resumed with a short scan, 29519r, that contained only 33 framesets. The flight system was still settling after slewing onto the survey track during this scan and all images are badly streaked. The first complete scans following this initial start-up were 29520r and 29521r at longitudes λ=9.35° and λ=209.58°, respectively. Because of the width of the NEOWISE focal plane, there were no true gaps in coverage on either side of the sky. However, the depth of coverage is reduced near λ=8.75° and λ=209.28° on the ecliptic equator.
In July 2024, the attitude rate fault occurred during scan 63658r centered along ecliptic longitude of λ=20.6°. The last complete scan prior to that was 63657r centered on λ=223.5°. Observations resumed with scan 63696r at longitude λ=21.4°, followed by scan 63698r at λ=224.8°. The survey interruption result in total coverage gaps of approximately 0.19° and 0.05 ° wide at the ecliptic equator on the two sides of the sky.
While not strictly survey interruptions, there are 10 NEOWISE Reactivation scans that had unrecoverable failures during data processing, and therefore are not found in the survey archives (04183s, 07944r, 15587s, 26843s, 34647r, 40823s, 45687r, 47591r, 62634r, and 63340r). Processing for these scans failed for a number of reasons. Most are short scans with too few framesets to enable useful dynamic calibrations (IV.2.a.ix). Some were the first scans taken following other survey interruptions and did not have all of the accompanying engineering telemetry and metadata that were required for processing. Finally, in a few scans the images are all badly smeared due to spacecraft motion and failed processing in the source extraction and position reconstruction steps.
These failed scans contain approximately 145 framesets. By comparison, successful processing was conducted for 26.88 million NEOWISE framesets during the Reactivation survey.
Last update: 21 November 2024


