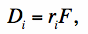IV. WISE Data Processing

6. Quality Assurance

d. Ancillary Notes

i. Noise Pixels

1. Introduction

We briefly review here the concept of the "effective number of noise pixels" N_p and present a general expression that can be used to derive N_p for any image of the Point Response Function (PRF). We define the PRF as the Point Spread Function (PSF) profile generated by the telescope optics alone convolved with the pixel response (accounting for any intra-pixel response variations), and resampled by the finite-sized pixels. The PRF and PSF are equivalent for a uniform intra-pixel response in the limit of infinite sampling. The terms PRF and PSF are often used interchangeably, and the distinction above is rarely made in astronomical imaging. Here we assume the PRF image was made a priori by combining and resampling a number of background-subtracted point source images. The better the PRF sampling, the more accurate the estimate of N_p.

In a nutshell, N_p is the effective number of pixels contributing to the flux-variance of a point source. Sometimes this is referred to as the number of pixels per beam. The bigger this number, the broader the PRF (hence the "poorer" the image quality or resolution), and the lower the sensitivity overall, i.e., fluxes will exhibit a larger variance on repeated observation. This should become clearer from the derivation below. The final result is given by Eq. 10 (boxed). In the end, think of N_p as a number that's more-or-less proportional to the square of the PRF effective width, e.g., see Eq. 13 for the simple case of a Gaussian PRF.

2. Derivation

The signal from a source with true flux F as measured in detector pixel i is given by:

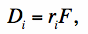(Eq. 1)

where r_i is the PRF volume normalized to unity: ∑_ir_i = 1. The r_i are usually estimated by combining point source profiles on an upsampled grid. For the derivation below, we assume the r_i were estimated on a grid with the same pixel size as the detector pixels. We will generalize to different pixel sizes for the r_i and D_i below. Furthermore, if R_i is the un-normalized point source response,

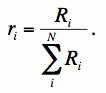(Eq. 2)

The true source flux F can be estimated from an unweighted linear least-squares by minimizing the cost function:

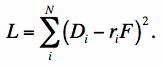(Eq. 3)

Differentiating Eq. 3 with respect to F and setting to zero, the least-squares solution is given by:

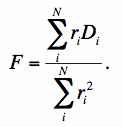(Eq. 4)

The noise-variance in F can be derived by adding errors to the true values in Eq. 4:

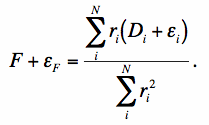(Eq. 5)

Subtracting true values, squaring, and taking expectation values, we have:

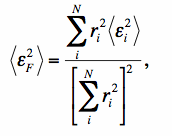(Eq. 6)

where we assumed the detector pixels are uncorrelated: <ε_iε_j> = 0 for i ≠ j. The noise-variance in the flux estimate F can then be written:

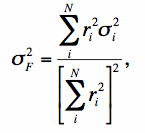(Eq. 7)

We now assume that the pixel variance σ²_i across a source is approximately constant and there exists some effective variance σ²_eff such that:

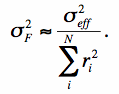(Eq. 8)

A constant variance is only true when the counts are dominated by a spatially uniform background and not when the counts are source-photon dominated. For the latter case, the σ²_eff corresponds to some average or intermediate value of the pixel variance across the source. From Eq. 8, the number of noise pixels N_p is identified with

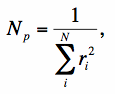(Eq. 9)

so that σ²_F ≈ N_pσ²_eff.

We include two generalizations to Eq. 9: first, the PRF values r_i may only be available in un-normalized form, e.g., as the R_i in Eq. 2; second, they may have been estimated on a much finer grid than the detector pixels. We would like to know the value of N_p for the detector pixels, not the PRF pixels. Using Eq. 2 and the fact that the PRF and detector pixel scales can be different, the number of noise pixels can be written:

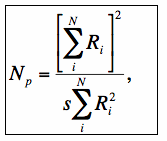(Eq. 10)

where s accounts for differences between the PRF (R_i) pixel size and the native detector pixel size. In general, this is the ratio of the native detector pixel area to PRF pixel area:

(Eq. 11)

where the CDELT1, CDELT2 refer to standard FITS header keywords for pixel scales along the X and Y axes respectively.

As a simple illustration, let's assume s = 1 and we have an un-normalized top-hat PRF spread over N pixels equal to constant value c. Equation 10 then gives:

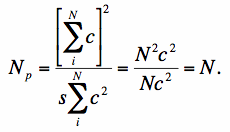(Eq. 12)

Therefore, for a top-hat PRF, the number of noise pixels is exactly equal to the number of pixels it spans. For a PRF with tails that decay fast enough, Eq. 10 will converge to some effective value characteristic of the PRF. For a Gaussian PRF, it is not difficult to show that

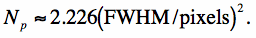(Eq. 13)

3. Results

Equation 10 was used to estimate the number of noise pixels for the WISE PRFs derived from survey data. Given the PRF for each band-array is non-isoplanatic, we have used the array center PRF from a 9 x 9 grid characterization. Results are shown in Table 1 where units are in #native detector pixels. The N_p estimates are in very good agreement with pre-flight values from optical modelling at SDL.

Last update: 2011 July 5