A Comparison of Responsivity Estimation Methodologies
Document number: WSDC D-T013

1. Overview

Below we summarize our results of estimating the relative responsivity (flat-field calibration) from a recent 30 orbit simulation provided by N. Wright. Two estimation methods were explored:

  1. The gradient (or slope) method implemented in the flatcal module. This method measures the amount by which each pixel responds to the change in overall (e.g., median) background level on a frame.

  2. The classic stacking (or standard) method implemented in the compflat module. This computes a trimmed average of a pre-conditioned stack of fames and normalizes the result by either a global median or a 2-D surface fit.
The goals are to determine: (i) the method which is most reliable at recovering the "true" flat-field calibrations used in the simulation, and (ii) the number of frames needed to achieve the desired flat-fielding accuracies in each band.

1.1 Summary

  1. Overall, there is little difference between the gradient and stacking method for bands 2, 3, and 4. For band 1, the stacking method wins hands down. For bands 2, 3, 4, one can delve into the statistics to attempt to pick the best method. If you don't want to read on, I'm inclined to go with the gradient method for these bands.

  2. In terms of relative uncertainties in the responsivity estimates (Tables 1 and 2), the stacking method appears superior over the gradient method in all bands for the same number of input frames. However, read on..

  3. These (data-derived) uncertainties don't provide a good handle on systematics (biases) with respect to "truth". The global median discrepancies from truth (over all pixels) are indeed smaller for the stacking method (Tables 3 and 4), but this is because the responsivity distributions are more symmetric than the gradient method (see histograms in Figures 6 - 8). The stacking method has more deviant pixels in the tails relative to truth. Therefore, the gradient method appears to be less biased for bands 2, 3 and 4 (in a global sense).

  4. It remains to be seen if band 2 shows similar variation in the background as simulated here to warrant use of the gradient method. If not, we will have to revert to the stacking method for band 2 as well.

  5. Tentative upper limits on the flat-fielding accuracy needed to satisfy photometric sensitivity requirements are summarized here. Overall, the desired flat-field accuracies are <~ 8, 3, 0.4, 0.3% for w1, w2, w3, w4 respectively. Taking the worst case uncertainties from Table 1 (as a conservative measure), this corresponds to requiring of order 500-700 frames for w1, w2, and 800-1200 frames for w3, w4.

  6. One long-standing speculation is whether the on-orbit illumination on the HgCdTe arrays will be enough to adequately fill the wells. This simulation indicates that flats for w1, w2 can be constructed to reasonable accuracy using the stacking method alone.

  7. Another concern is the presence latent-sources contaminating the responsivity maps. These are actually seen in the w3 and w4 maps (see Figures 3 and 4 - challenge yourself to find them!). If these are ~constant and persist for the duration over which a particular flat is created/applied, then these artifacts should divide out.

2. Relative % Uncertainty vs. Number of Scans

This is defined as the median of 100*(σf / f) over all pixels where σf is the 1-sigma uncertainty in the resposivity estimate f for a pixel. This quantity is shown as a function of the number of input scans. Note that 1 scan ~ 250 frames, so 8 scans ~ 2000 frames. Table 1 shows results for for the gradient method and Table 2 for the stacking method.

Band 1 scan 2 scans 3 scans 4 scans 5 scans 6 scans 7 scans 8 scans
1 11.407 6.892 5.895 4.870 4.479 3.976 3.755 3.443
2 4.582 2.787 2.380 1.970 1.809 1.608 1.517 1.392
3 0.385 0.261 0.216 0.184 0.166 0.150 0.140 0.130
4 0.392 0.270 0.222 0.190 0.171 0.155 0.144 0.134
Table 1: Relative % uncertainties for the gradient method

Band 1 scan 2 scans 3 scans 4 scans 5 scans 6 scans 7 scans 8 scans
1 2.908 2.131 1.719 1.506 1.337 1.228 1.132 1.063
2 0.763 0.549 0.445 0.388 0.345 0.316 0.292 0.274
3 0.098 0.070 0.057 0.049 0.044 0.040 0.037 0.035
4 0.115 0.083 0.067 0.058 0.052 0.048 0.044 0.041
Table 2: Relative % uncertainties for the stacking method

3. Relative % Difference from Truth vs. Number of Scans

This is defined as the median absolute difference with respect to "truth": 100*median(|fest - ftrue| / ftrue), where fest is the estimated (measured) responsivity for a pixel and ftrue is the true value from the flat-field used for the simulation. The median is over all pixels in the flat-field. This quantity is shown as a function of the number of input scans. Note that 1 scan ~ 250 frames, so 8 scans ~ 2000 frames. Table 3 shows results for for the gradient method and Table 4 for the stacking method.

Band 1 scan 2 scans 3 scans 4 scans 5 scans 6 scans 7 scans 8 scans
1 13.754 10.887 10.370 10.300 10.178 10.254 10.174 10.238
2 3.361 1.993 1.701 1.412 1.292 1.157 1.084 1.001
3 0.287 0.199 0.167 0.142 0.131 0.117 0.111 0.103
4 0.285 0.212 0.175 0.156 0.141 0.131 0.122 0.115
Table 3: Relative % difference from truth for the gradient method

Band 1 scan 2 scans 3 scans 4 scans 5 scans 6 scans 7 scans 8 scans
1 2.294 1.758 1.475 1.340 1.233 1.172 1.112 1.076
2 0.565 0.420 0.351 0.314 0.286 0.269 0.254 0.243
3 0.068 0.049 0.040 0.035 0.032 0.029 0.027 0.026
4 0.081 0.058 0.048 0.042 0.038 0.035 0.032 0.031
Table 4: Relative % difference from truth for the stacking method

4. Responsivity Map Comparisons

All assume 2-scans worth of frames (1 orbit or ~ 500 frames).

Figure 1 - Band 1: From left to right: Flat estimated from gradient method; from stacking method; and truth used in simulation. Click to enlarge.

Figure 2 - Band 2: From left to right: Flat estimated from gradient method; from stacking method; and truth used in simulation. Click to enlarge.

Figure 3 - Band 3: From left to right: Flat estimated from gradient method; from stacking method; and truth used in simulation. Click to enlarge.

Figure 4 - Band 4: From left to right: Flat estimated from gradient method; from stacking method; and truth used in simulation. Click to enlarge.

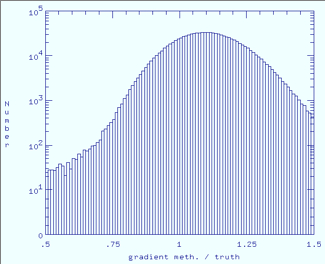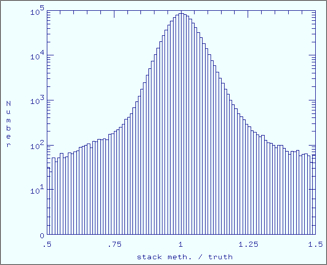5. "Estimated / Truth" Responsivity Histograms

Gradient method / Truth Stacking method / Truth
Figure 5 - Band 1 histograms of ratio of estimated to true responsivity map for each method. Click any panel to enlarge.

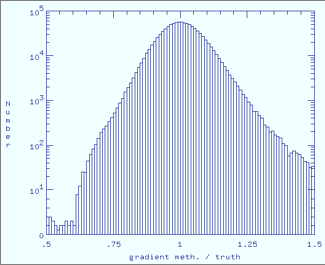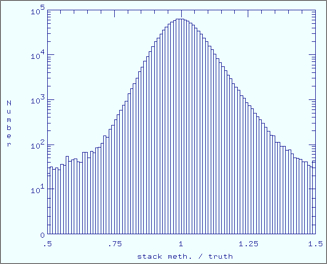Gradient method / Truth Stacking method / Truth
Figure 6 - Band 2 histograms of ratio of estimated to true responsivity map for each method. Click any panel to enlarge.

Gradient method / Truth Stacking method / Truth
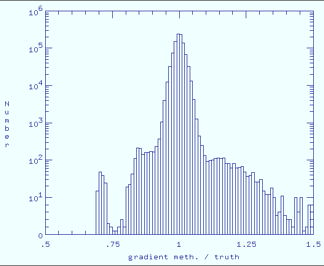
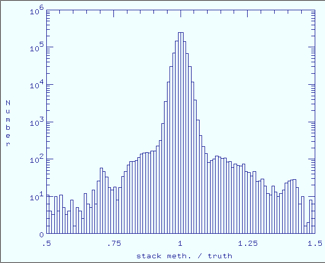
Figure 7 - Band 3 histograms of ratio of estimated to true responsivity map for each method. Click any panel to enlarge.

Gradient method / Truth Stacking method / Truth
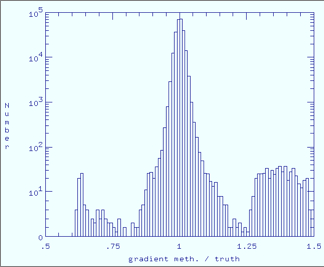
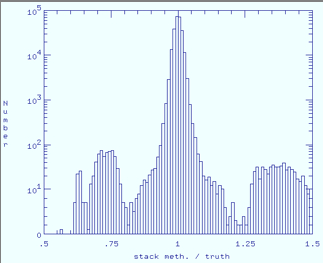
Figure 8 - Band 4 histograms of ratio of estimated to true responsivity map for each method. Click any panel to enlarge.


Last update - 6 August 2009
F. Masci - IPAC