Coverage Simulations for Band 2 Candidate Array (fpa143)

I. Introduction

We present simulated depth-of-coverage maps using bad-pixel masks constructed from a WISE band-2 (4.7μm) candidate array. This is referred to as detector "FPA143" in the test suite.

The simulations below are a continuation of those for a previous band-2 candidate (FPA141): Coverage Simulations for Band 2 Candidate Array (fpa 141). Below we adopt the same assumptions, methodology and software as presented therein.

Inputs

The main input is a bad pixel mask image provided by the WISE Science Project Office. This was recieved as a 1024x1024 FITS image with bad pixels denoted with a value "1", and good pixels denoted with value "0".

For FPA143, bad pixels were identified using the same criteria as outlined in Coverage Simulations for Band 2 Candidate Array (fpa 141). For your informaion, ~5.2% of pixels in FPA143 (in the active region) are declared as bad.

Figure 1 - Left: bad-pixel mask from FPA143 provided by project office. Right: same mask after smoothing with an interpolation kernel (see below for details). Click on image to enlarge.

These masks can be downloaded in FITS format here:

bad_pix_tot143

bad_pix_tot143_smoothed

II. Results

We performed two simulations, each consisting of 100 (15-orbit) coverage realizations, corresponding to two bad-pixel masks: one using the default mask, and another using the same mask but smoothed with an interpolation kernel.

We present below coverage fractions, maps and histograms computed from the 100 realizations. These statistics represent the fraction of pixels (or area) within a simulated 2048x1024 central region with that depth-of-coverage. The means are computed over all realizations. The coverage maps represent those whose coverage fractions fall closest to the mean fractions.

1. Test Run #1 (Default Mask)

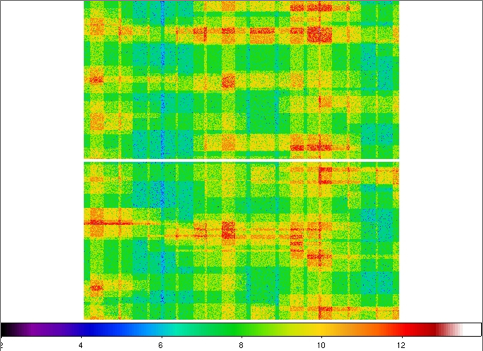
cov.  mean fraction (0 degrees)
3   0.00000999
4   0.00066078
5   0.00764946
6   0.05194377
7   0.18636921
8   0.29444338
9   0.25664891
10  0.13692860
11  0.04887179
12  0.01289172
13  0.00277685
14  0.00058730
15  0.00017820
16  0.00003998

cov.  mean fraction (90 degrees)
3   0.00000599
4   0.00075568
5   0.00851748
6   0.05494734
7   0.18695492
8   0.29097404
9   0.25009989
10  0.13743634
11  0.05160872
12  0.01467195
13  0.00306873
14  0.00072192
15  0.00020361
16  0.00003331

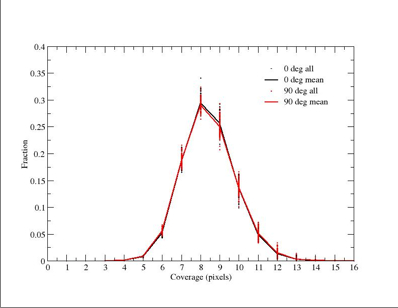
Figure 2 - Coverage maps for Test 1 (default mask): top = 0 degrees; bottom = 90 degrees.	Figure 3 - Coverage distributions for Test 1 (default mask).
Left: false color JPEG images of coverage maps for the default mask. The color bar at the bottom corresponds to the approximate coverage depth. Right: corresponding coverage distribution with fractions normalized to unity. Dots represent the 100 individual realizations. The lines go through the mean fractions from all realizations. Click on thumbnails to see full-size JPEG maps.

Summary

• For the default FPA143 bad-pixel mask that uses all the "bad" criteria, up to ~53% of an area on the ecliptic equator (the mean at 0 or 90 degrees) will have fewer than 8 coverages. <0.1% will have fewer than 4 coverages.
• As a reminder, a minimum coverage of 4 over at least 95% of the whole sky is the mission requirement. But note, our simulation area effectively represents ~0.7% of the sky centered on the ecliptic equator when compared to the full ecliptic latitude range [-90 to 90 degrees].
• The mode coverage is ~8. The RMS scatter about the mean fraction at this value is ~ +/-2% (both 0 and 90 degrees) and is representative at other coverages;
• For 100 realizations, the standard error in the mean fractions quoted above is of order RMS/sqrt(100) ~ +/-0.2%;

2. Test Run #2 (with Kernal Smoothing)

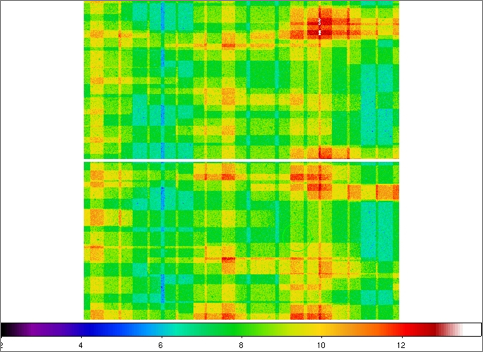
cov.  mean fraction (0 degrees)
5   0.00110773
6   0.03402189
7   0.18148174
8   0.31263049
9   0.27185920
10  0.13863895
11  0.04686083
12  0.01100237
13  0.00189554
14  0.00039498
15  0.00010622

cov.  mean fraction (90 degrees)
5   0.00126862
6   0.03833573
7   0.18414788
8   0.30641195
9   0.26448227
10  0.13944702
11  0.05042518
12  0.01257930
13  0.00228832
14  0.00048372
15  0.00010496
16  0.00002499

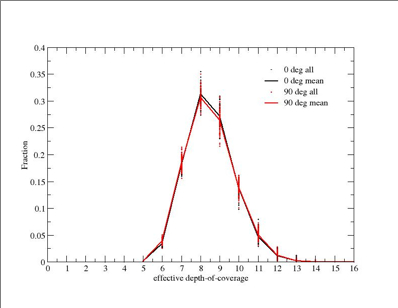
Figure 4 - Coverage maps for Test 2: top = 0 degrees; bottom = 90 degrees.	Figure 5 - Coverage distributions for Test 2.
Left: false color JPEG images of coverage maps for Test 2 (including smoothing from an interpolation kernel). The color bar at the bottom corresponds to the approximate coverage depth. Right: corresponding coverage distribution with fractions normalized to unity. Dots represent the 100 individual realizations. The lines go through the mean fractions from all realizations. Click on thumbnails to see full-size JPEG maps.

Summary

• For the same FPA143 bad-pixel mask convolved with a model interpolation kernel, up to ~53% of an area on the ecliptic equator (the mean at 0 or 90 degrees) will also have fewer than 8 coverages. There are no areas with fewer than 4 coverages;
• The mode coverage is ~8. The RMS scatter about the mean fraction at this value is ~ +/-2.5% (both 0 and 90 degrees) and approximately representative at other coverages;
• For 100 realizations, the standard error in the mean fractions quoted above is of order RMS/sqrt(100) ~ +/-0.25%;

III. Conclusions

• Given the default FPA143 (band-2) bad-pixel mask, <0.1% of an area on the ecliptic equator will have fewer than 4 coverages, and ~53% will have fewer than 8 coverages (see Figure 3). The simulated area effectively represents ~0.7% of the sky.
• With inclusion of smoothing from an interpolation kernel as represented by a model PRF fit, there are no areas with coverage depths <5, while ~53% will still have fewer than 8 coverages (see Figure 5). For your information, interpolation kernels will be used for optimal Atlas image generation.
• The reason for these slight (but significant) drops in areas with low-coverage when kernel smoothing is present is due to a "smearing" of good pixel information into adjacent bad pixels (mainly because there are more good pixels than bad ones). This effectively increases the depth-of-coverage at the locations of bad pixels on the sky.
• The impact of an interpolation kernel on increasing the effective depth-of-coverage at bad pixels is maximized if the bad pixels are more-or-less randomly distributed as single isolated pixels. If the same number of bad pixels were in larger concentrations, a large fraction would be shielded by the PRF tails of good pixels and thus, the average depth-of-coverage is expected to decrease.
• Note: the above does not mean that bad pixels can be completely mitigated by the smearing effect of the PRF. There is still a net loss of information when bad pixels are present in that the effective coverage is slightly lowered at the location of good pixels that are next to bad ones. Also, smearing by the PRF itself results in reduced point source sensitivity by an amount proportional to the square root of the equivalent number of "noise pixels" contributing to a flux measurement. The number of noise pixels is characteristic of the PRF. For more details on kernel smoothing and noise pixels, see: Use of Smoothing Kernals.