Circular and Fixed Elliptical Apertures: The Petrosian and Isophotal Photometry

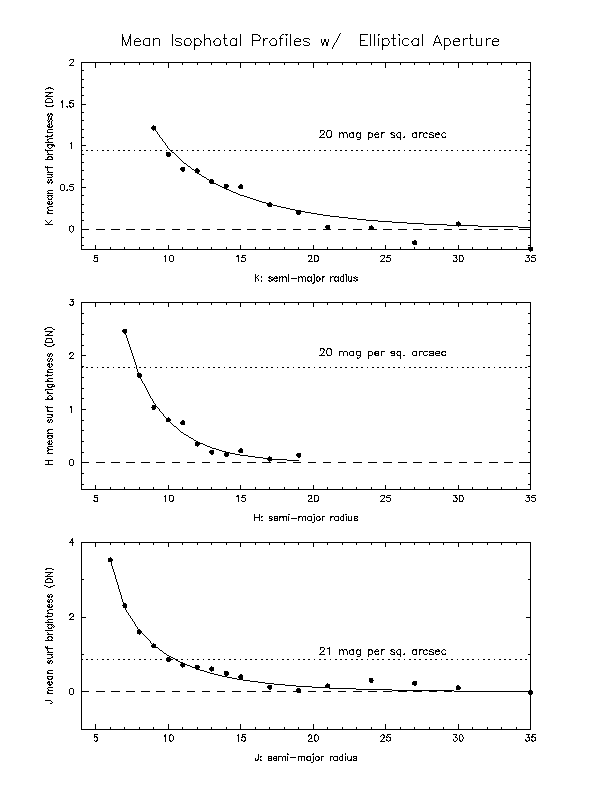
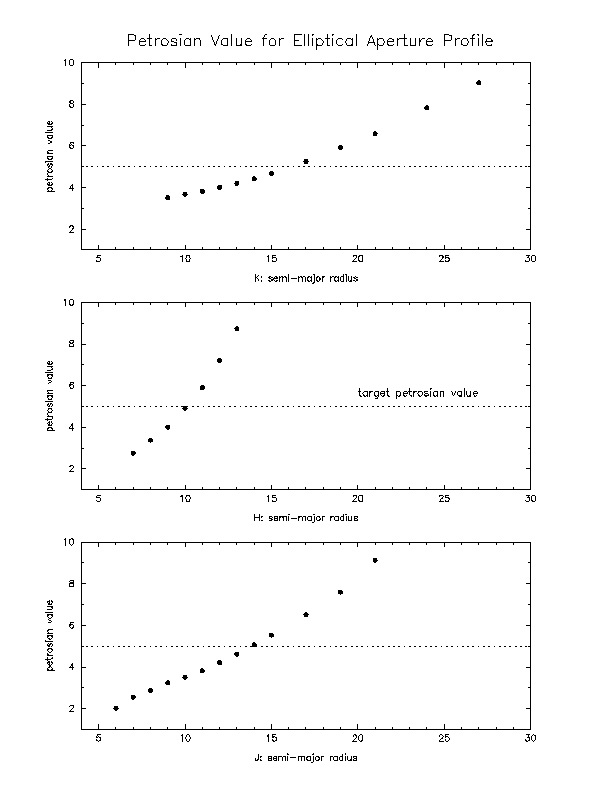
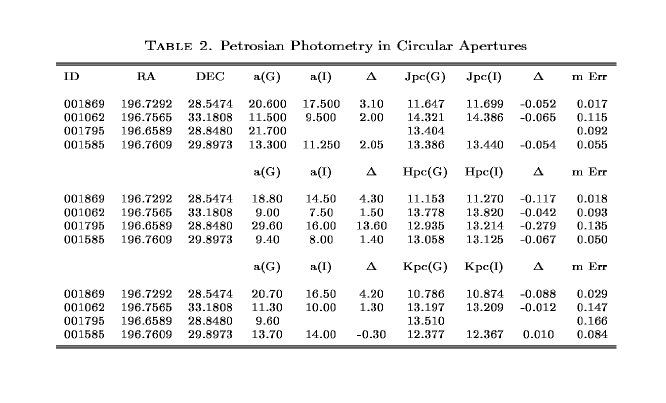
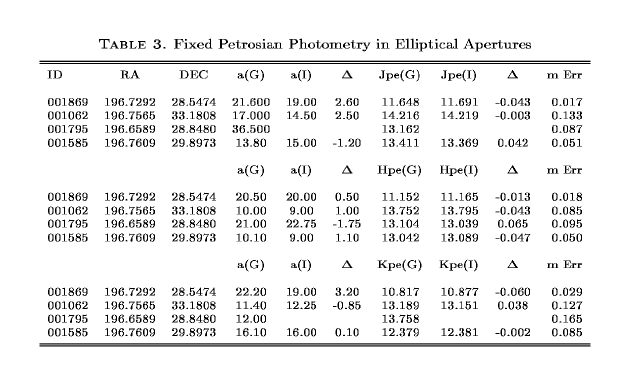
The second of the photometric tests ran was to determine the petrosian magnitudes of the four galaxies in fixed circular and elliptical apertures. We define the petrosian radius to be the point where the ratio of the mean brightness in an aperture to the mean isophotal brightness becomes 5.0. The comparison between the GALWORKS and IRAF magnitudes for the circular apertures are given in Table 2, and for elliptical apertures in Table 3. The circular values in IRAF were determined by fixing the apertures at the GALWORKS center position and looking, by eye, for the point where the petrosian value becomes five. GALWORKS determines this point by first fitting a modified exponential to the isophotal profile, then performing the ratio of mean surface brightness to the fitted isophotal brightness, and finally linearly interpolating to arrive at the petrosian radius (see Figures 2a and 2b). Table 2 shows that significant differences can arise when fitting a curve to the data rather than selecting the first point where the ratio becomes five. Columns 3-5 are the petrosian radii for GALWORKS and IRAF and the difference between the two repectively. The next three columns are the corresponding magnitudes, and the final column is the GALWORKS quoted magnitude error. Table 3 is the same as Table 2 for elliptical apertures. The elliptical values presented are for the case of the center positions, ellipticities, and position angles fixed (see Appendix A for a description of the IRAF vs. GALWORKS standards for these values) at the GALWORKS values. Tables 2 and 3 show that the determination of the petrosian value can be fairly dependant on the method used to determine it. Fitting a function to the data should provide a more robust solution for the petrosian value as shown in Figures 2a and 2b. One of the main problems with the eyeball estimate is that the results can be tremendously effected by the binning of the data. The difference in the sizes of the apertures determined by the two different methods result in large differences in the photometry. For example, note that Table 2 shows large differences between the IRAF and GALWORKS magnitudes for galaxy 1795 due to the large differences in derived petrosian radii, but the difference between the radii is small in Table 3 for the case of elliptical apertures and hence the magnitude difference is also small. The difficulty in using circular apertures, in this case, arises at least partially from the galaxy being elliptical, not circular.

The IRAF magnitudes at the GALWORKS selected petrosian and isophotal radii have been determined and are included in Appendix B. The results are similar to those for the fixed radius circular apertures with errors of a few percent. As with the circular apertures, the differences are due to fractional pixels used by GALWORKS.

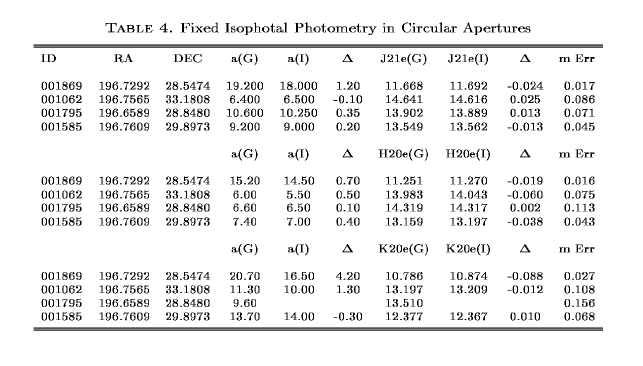
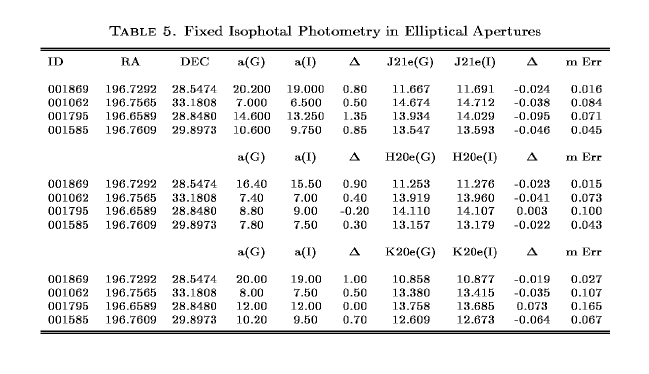
For the isophotal photometry we have done an analysis similar to that for the circular and fixed elliptical petrosian values. Tables 4 and 5 show the isophotal photometry for the circular and fixed elliptical apertures respectively. The J-band photometry are determined for the 21 mag/sq. arcsec isophote while the H- and K-band photometry are determined for the 20 mag/sq. arcsec isophote. What is apparent in both of these cases is that the difference in the determination of the radius causes a magnitude error of a few up to ten percent in the worst case. It appears that the errors are slightly smaller than in the petrosian case, but it is hard to say definitively with only four galaxies. Again here we believe that the modified exponential fit which GALWORKS uses to determine the isophotal radius is a more robust than the crude eyeball estimate used on the IRAF data.