The effect of PSF smearing
on WISE profile-fitting photometry

WSDC D-T018

I. Introduction

The attitude of the WISE spacecraft is stabilized by a pair of star trackers. If both are functioning, the pointing is expected to be sufficiently stable that no appreciable drift will occur during an integration period. If one of the star trackers is disabled, however, significant drift could occur, resulting in a smearing of point spread function (PSF). The purpose of this study is to assess the degree to which this smearing biases the fluxes estimated during profile-fitting photometry.

II. Procedure

The basic procedure in these simulations was similar to that used in our previous Investigation of WPHot flux biases.
The difference in this case, however, was the use of smeared PSFs in data generation. Specifically, synthetic data were generated for an 11x11 set of isolated point sources on a sky background with Gaussian additive noise, with the source images being smeared uniformly along a straight line whose length was varied. Profile-fitting source extraction was then carried out using unsmeared PSFs, and the resulting magnitude differences (estimated - true) determined for various smearing lengths and signal to noise ratios. The PSFs used in the present study were those from a multi-orbit simulation by N. Wright in May, 2009. From those simulations we generated a 5x5 grid of PSFs covering the focal plane, and have been using them to test our data processing pipeline. Figure 1 shows a sample PSF, uncertainty map, and smeared PSF.

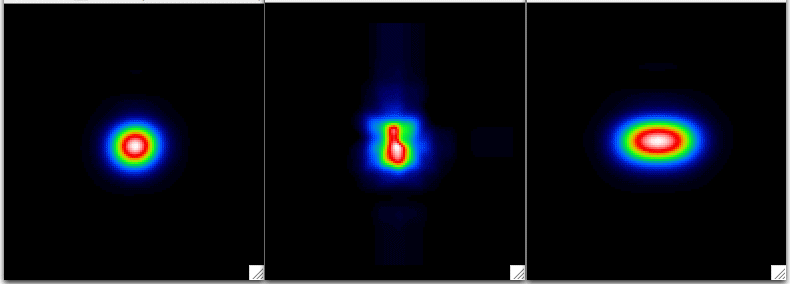Fig 1: Left: Central PSF in band 1; Center: PSF uncertainty (peak value = 1.5% of PSF peak); Right: PSF smeared by 10 arcsec. The field of view is 22 arcsec and the intensity scale is linear.

III. Results

Figure 2 shows a plot of the Band 1 magnitude bias a function of signal to noise ratio (SNR) in the absence of smearing. For a more detailed discussion on the peculiarities of this plot, please see Investigation of WPHot flux biases.

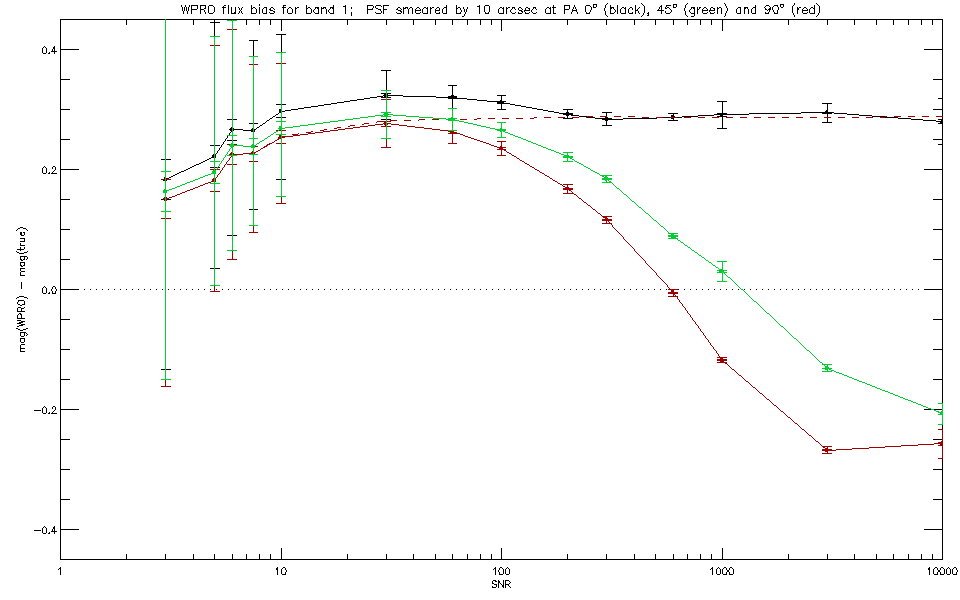Fig 2: WPHot/WPRO flux bias in the absence of PSF smearing. The outer error bars represent the standard deviations of individual estimates; the inner error bars represent the standard deviation of the mean.

Figure 3 below shows the flux bias in band 1 as a function of SNR for a smearing length of 10 arcsec. The solid curves represent the results for three different position angles of smearing: black = 0 deg (i.e., smearing along y-axis), green = 45 deg, and red = 90 deg.

Fig 3: Photometric flux bias at band 1, resulting from PSF smearing. .

The red curve was obtained using the smeared PSF shown in the right-hand panel in Figure 1; the unsmeared version of the curve is shown in Figure 2. It is apparent that the bias is of opposite sign for low SNR as compared to high SNR. This behavior is due to the non-uniform weighting resulting from PSF error, represented by the PSF uncertainty map in the center panel of Figure 1. When the photometry is repeated using uniform weighting (corresponding to uniform background noise and zero PSF uncertainty), the red dashed line in Figure 3 is obtained. The bias is then approximately constant over the full range of SNR. Normally what happens is that the flux is underestimated when the PSF is too small, but this becomes reversed when the PSF uncertainty has a compact localized peak. The reason is that the data are then de-emphasized in the central portion of the PSF, allowing a least squares fit with higher source flux.

Because of the latter effect, asymmetries in the PSF uncertainty map cause the photometric bias to be dependent on the position angle of the smearing in the high-SNR regime (the regime in which PSF errors dominate). The red curve in Figure 3 represents one extreme of this. The other extreme is represented by the black curve in Figure 3, whereby the smearing is in the y-direction, i.e., along the direction of elongation of the PSF uncertainty. The green curve represents the intermediate case, i.e. a position angle of 45 deg.

Figure 4 shows the photometric bias as a function of smearing length for all four bands. A standard SNR value of 30 was chosen for this plot, since it is in the background-dominated regime, relatively free from the vagaries associated with geometric effects with the PSF uncertainty.

Fig 4: Photometric flux bias as a function of smearing length. The assumed values of SNR and position angle of smearing were 30 and 45 deg, respectively. The solid curves are for band 1 (black), band 2 (blue), band 3 (green), and band 4 (red). These results correspond to a PSF in the central portion of the array. For comparison, the dashed and dotted curves are for band-1 PSFs in two of the array corners ([x=1,y=1] and [x=5,y=1] of a 5x5 array, respectively).

This figure shows that the background-dominated regime, the fluxes of the smeared sources are, for the most part, underestimated by a factor which increases with smearing length, as expected. It also suggests that the flux bias is affected very little by the variation in PSF shape in going from the center of the array to the edges, at least for the distortion parameters assumed during the simulations.

In Figure 5, the (estimated - true) magnitude differences for each band have been replotted as a function of smearing length expressed as a fraction of the effective width of the PSF (6.63, 7.11, 9.49, 15.31 arcsec for the present PSFs in bands 1-4, respectively), where the effective width is defined as the square root of 4/pi times the volume to height ratio. It is apparent that the normalization by PSF width has brought the curves together, i.e., the flux bias is, to a good approximation, dependent only on the ratio of smearing length to PSF width, and is otherwise band-independent.

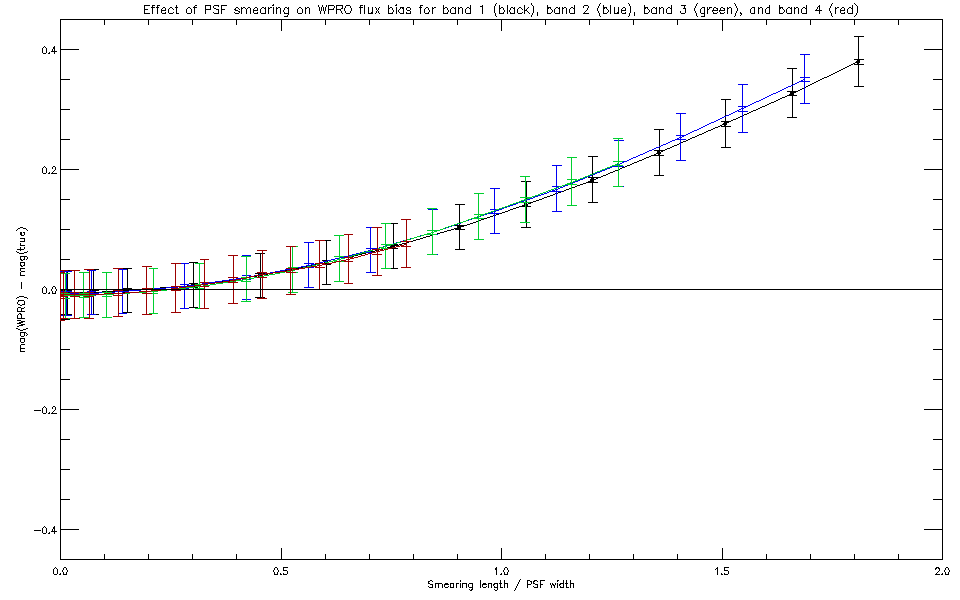Fig 5: Photometric flux bias as a function of smearing length expressed in units of the effective width of the PSF.

The corresponding variation of reduced chi squared for each band is shown in the next figure.

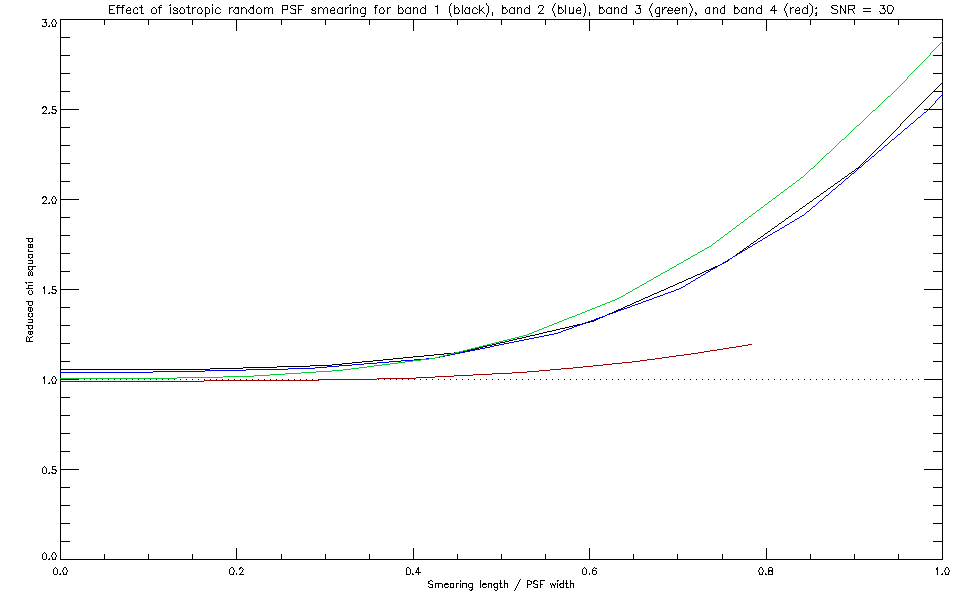Fig 5b: Reduced chi squared as a function of relative smearing length for SNR = 30.

The next figure illustrates how the reduced chi squared varies with SNR for a given smearing length (in this case, equal to half of the PSF width):

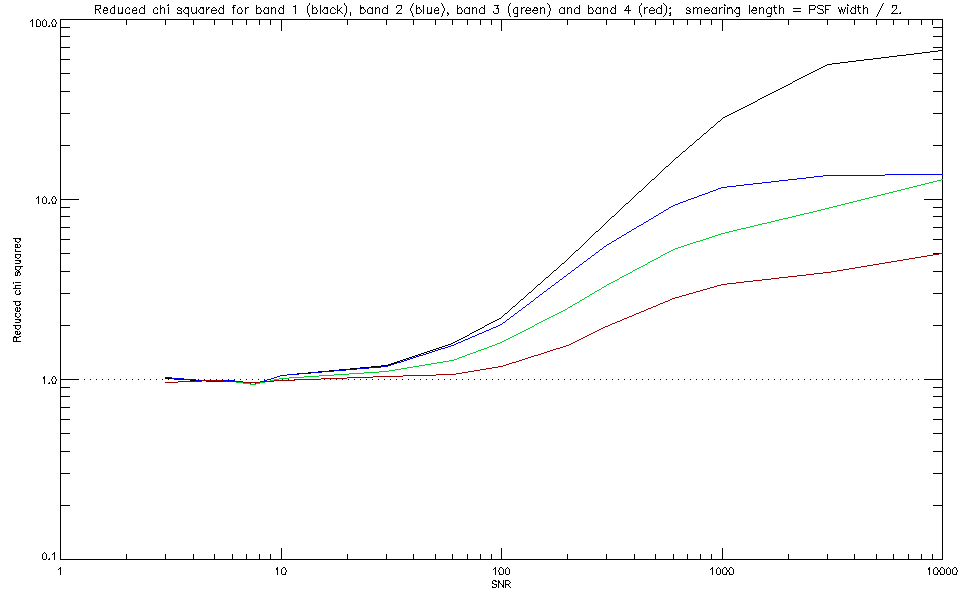Fig 5c: Reduced chi squared as a function of SNR for a smearing length equal to half of the PSF width at each band.

Differences in the behavior of reduced chi squared for the different bands (both as a function of smearing length and SNR) are due to differences in the PSF uncertainty maps. For example, at large SNR, the reduced chi squared becomes dominated by the PSF error term in the noise model, and for the present PSF set this tends to be larger for the longer wavelength bands. This is reflected in the lower values of reduced chi squared for band 4 in Figure 5c.

IV. Conclusions

For the particular set of PSFs currently being used in WISE simulations:

1. At a given band, the flux bias increases monotonically with smearing length, as expected.

2. In the high SNR regime, the bias is strongly influenced by the details of the PSF uncertainty map, and is therefore dependent on the direction of the smearing.

3. At low to moderate SNR (where Poisson noise dominates), the flux is systematically underestimated, reaching almost 20% at band 1 for a smearing length of 8 arcsec. The severity at the other bands scales closely in inverse proportion to the PSF width.

4. The bias is not strongly influenced by the location of the PSF on the focal-plane array.

5. The reduced chi squared increases with smearing length, as expected. The rate of the increase is dependent on the signal to noise ratio and the band-dependent PSF uncertainty.

V. The Effect of Isotropic Smearing

The above results pertain to the case in which the PSF is uniformly smeared along a straight line of specified length. We now consider the case in which the PSF is smeared isotropically by random jitter. Specifically, we consider the case where the PSF is subject to Gaussian random position offsets, uncorrelated in the x and y directions, and define our smearing scale as the RMS radial offset (i.e., RMS positional jitter), equal to sqrt(2) times the sigma of position error in either x or y.

1. The effect on flux bias

Figure 6 shows the effect on the flux bias as a function of smearing scale at each of the four bands.

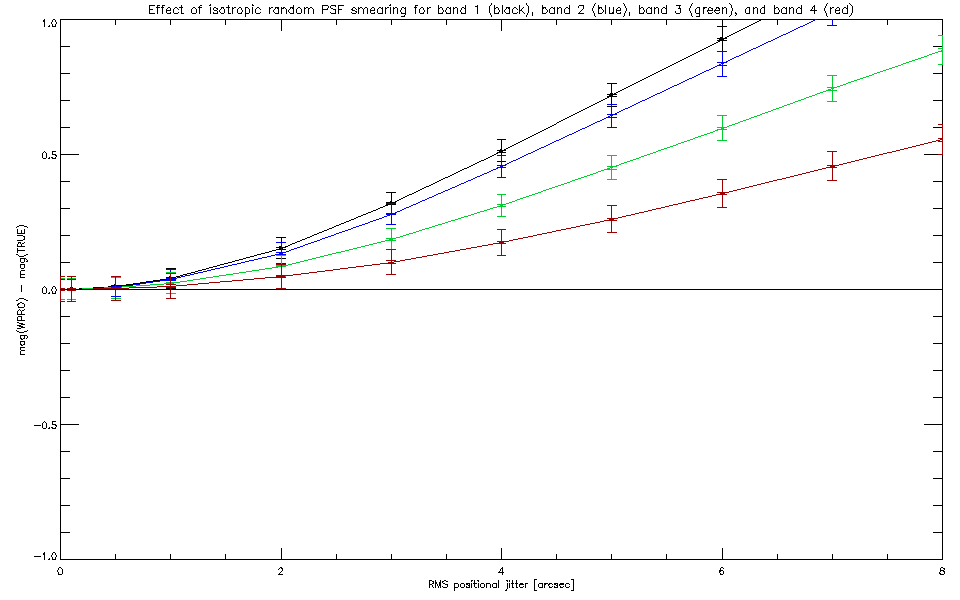Fig 6: Photometric flux bias due to isotropic smearing of the PSF, for SNR = 30.

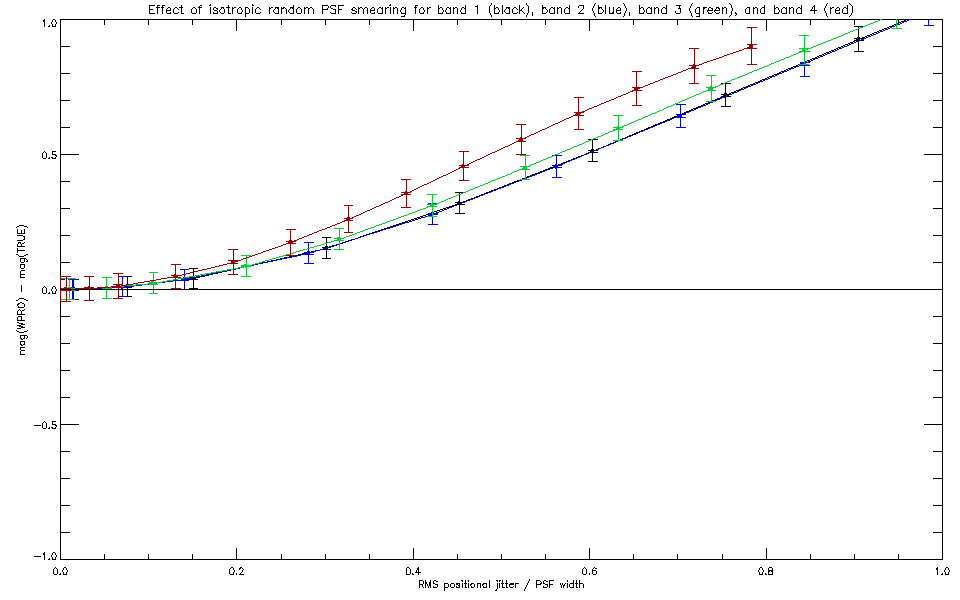Re-plotting with the horizontal axis in units of the PSF width gives:

Fig 7: Photometric flux bias due to isotropic smearing of the PSF as a function of smearing scale in units of the PSF width. The assumed SNR was 30.

Just as for the linear smearing case, the flux bias is, to a reasonably good approximation dependent on the ratio of smearing scale to PSF width, and is otherwise more or less band-independent.

For comparison, the result for large SNR is shown in the next figure.

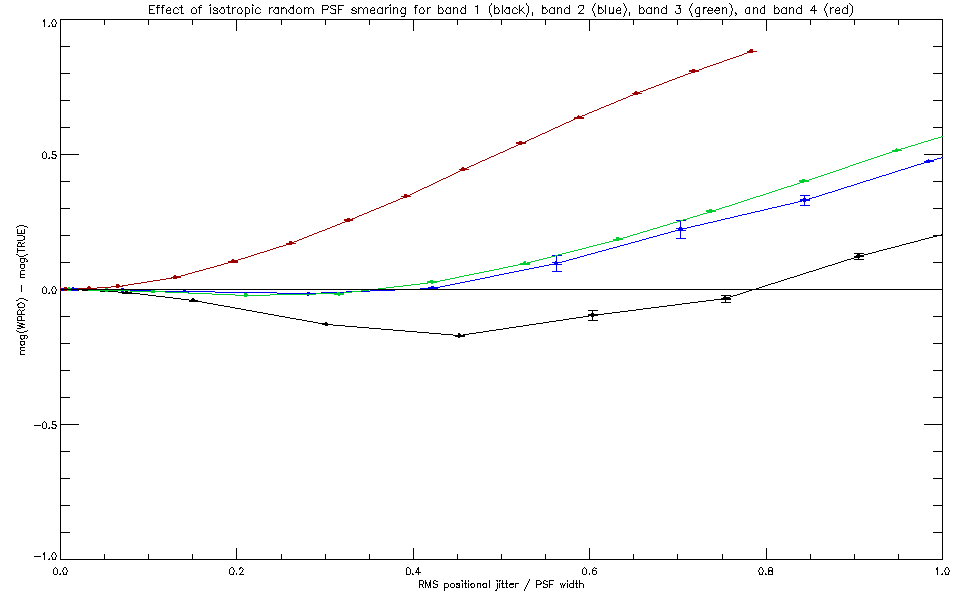Fig 8: Photometric flux bias due to isotropic smearing of the PSF as a function of smearing scale in units of PSF width. Large SNR case.

The behavior in this case is clearly more complicated, and is due to the interaction between the PSF broadening and the non-uniform weighting due to the spatial variation of PSF uncertainty. The simple band-independent variation of flux bias with the ratio of smearing scale to PSF width has been destroyed by the band-to-band differences in the uncertainty maps.

2. The effect on chi squared

The next two figures show the reduced chi squared as a function of normalized smearing scale for the moderate and high SNR cases, respectively.

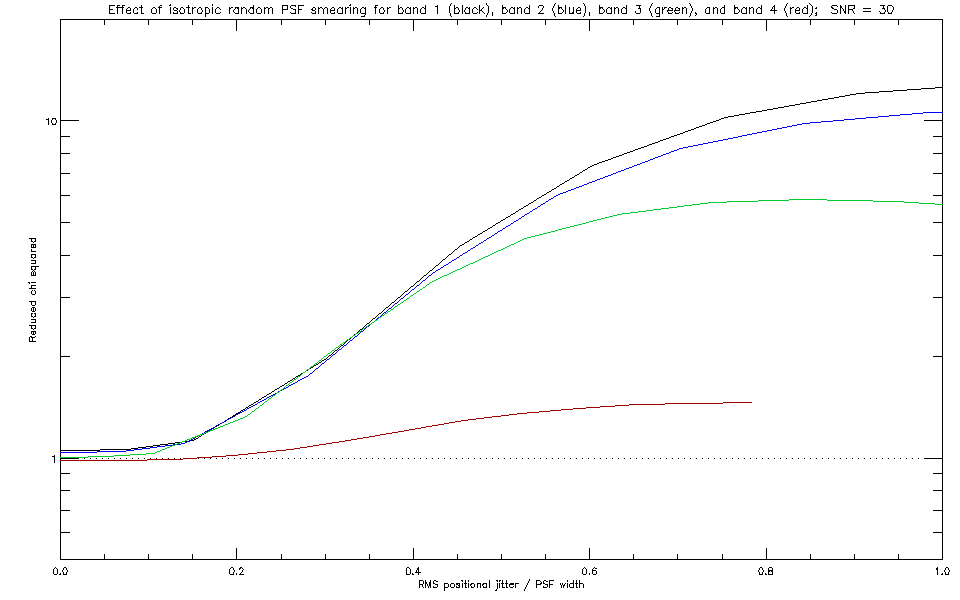Fig 9: Reduced chi squared as a function of normalized smearing scale for SNR = 30.

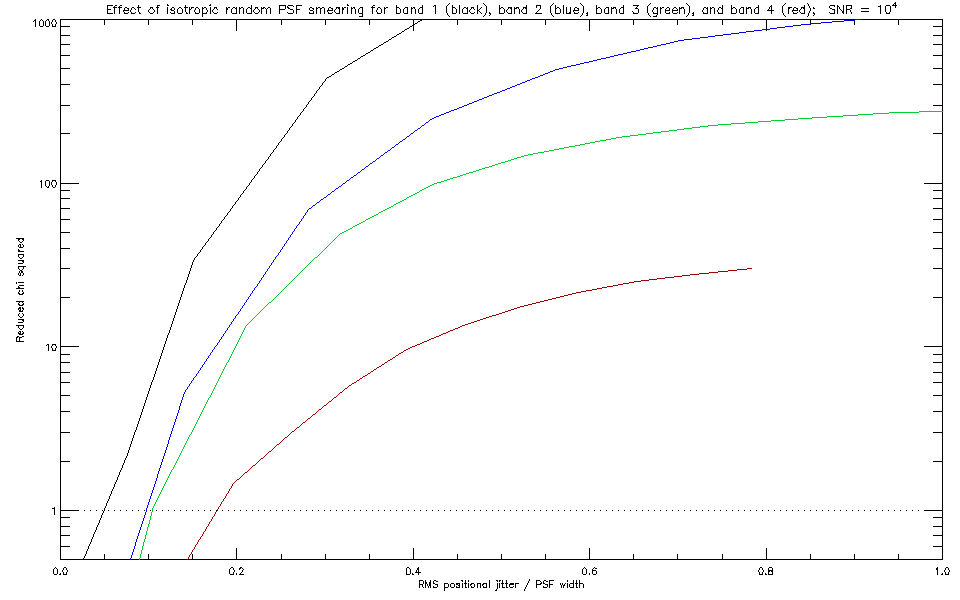Fig 10: Reduced chi squared as a function of normalized smearing scale for large SNR.

Not surprisingly, the reduced chi squared rapidly gets large as the smearing scale increases, the effect being much more severe for the high SNR (PSF error dominated) case. Note that for the latter case, the reduced chi squared starts off at a value much less than unity. The reason is that for these simulations, a constant PSF was used in the generation of the synthetic data; random PSF variations were not simulated, so essentially a perfect fit is obtained in the case of zero smearing at high SNR. By contrast, the reduced chi squared for the Poisson-noise dominated case (SNR = 30) starts out close to unity at all bands. It is interesting that in the latter case, the reduced chi squared is not very much affected by PSF smearing until the smearing scale reaches about 0.15 of the PSF width.

3. Discussion

Comparison with the linear smearing results shows that the effects of isotropic smearing are far more severe. For example, Figure 7 indicates that for an RMS positional jitter of half the PSF width, the magnitude bias is 0.4. This level of jitter corresponds to a smearing function whose FWHM is 0.83 of the PSF width. Comparing this with Figure 5 shows that the magnitude bias for the equivalent amount of linear smearing is approximately 0.1, i.e. a factor of 4 less severe. This factor holds for other values of smearing length also.

Conclusion:

Isotropic smearing by a Gaussian function at representative values of SNR produces a photometric bias of about 4 times that obtained for the equivalent amount of uniform linear smearing.

Last update - [2009 Oct 26]
K. A. Marsh (IPAC)