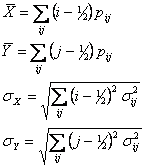 |
(Eq. 1) |
One image-quality metric used for QA is the degree of circularity of the point-source images. This metric is evaluated in each of the four bands. A list of point-source extractions in the band is provided for each frame, and postage stamps are cut out of the images for normalizing and averaging. For a complete scan, the postage stamps from all frames in the scan are used.
The postage stamp for each point source is a 9×9 grid whose center pixel contains the point-source position. Each postage stamp is background-subtracted, volume normalized, and projected into a 3×3 oversampling grid (hence a 27×27 grid) before being used in the averaging. By default, the background level is taken to be the median value of the postage stamp's outer-rows/outer-columns pixels.
Volume normalizing requires that there be no missing pixels in the 9×9 postage stamp, but a large fraction of such postage stamps have bad pixels. This fraction was found to be too large simply to discard. When masked pixels are encountered, by default their values are interpolated from the neighboring pixels. An exception is that the central pixel cannot be interpolated linearly, so if it is masked, the postage stamp is rejected. Otherwise bilinear interpolation is used; higher order or template fitting is not used in order to minimize bias toward expected PSF shapes. This amounts to averaging opposite neighbors, with diagonal neighbors weighted 1/√2 as much as horizontal/vertical neighbors. By default, all four pairs of neighbors must be available, i.e., not contain any masked pixels themselves, otherwise the postage stamp is rejected.
Because the W4 PSF has a significant Airy ring around the main PSF, the bilinear interpolation is not optimal, and instead a radial median was used to replace masked pixels. Radial medians are computed at all rounded-off integer-pixel radial distances from the center pixel and used for masked pixels at the same radial distance. This cannot be used for the center pixel.
Some additional filtering was employed to reject cases in which: (a.) background subtraction left an excessive number of significantly negative pixels; (b.) pixels in the outer two rows and columns had excessively high values, indicating confusion with nearby sources.
The 9×9 postage stamp may be projected into the 27×27 oversampling grid in two ways, each of which begins by aligning the sub-pixel estimate of source position over the central oversampling pixel that contains it: (a.) interlaced mode copies the 9×9 pixels into the subset of the 27×27 pixels lying directly beneath them; (b.) smoothed mode projects each of the 9×9 pixels into all 9 of the 3×3 oversampling pixels directly below tyhem. The latter results in smoothing the oversampled PSF with the array-pixel response function. By default, interlaced mode was employed for QA.
Postage stamps judged acceptable in a given band were averaged in two ways: (a.) all postage stamps together; (b.) partitioned into separate averages according to array location. For item (b.), uniform 5×5 partitioning of the array was employed. This was intended to help reveal PSF variation over the array.
Each type of averaging was done in two passes: (a.) an initial pass in which means and standard deviations were computed for each of the 27×27 oversampling pixels; (b.) a second pass in which samples more than 2σ from the first-pass average were rejected.
After the averaging has been completed, each of the 27×27 PSFs is characterized in terms of size and shape as follows, where pij is the volume-normalized PSF pixel value in row i and column j, and σij is the uncertainty in pij. The centroid position and uncertainty on each axis is computed:
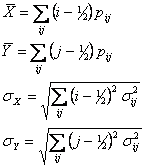 |
(Eq. 1) |
The uncertainty formulas assume that the pixel errors in the 27×27 PSF are uncorrelated, which is a somewhat coarse approximation, but bookkeeping the correlations in order to improve the approximation does not appear cost-effective. Next, the second moments are obtained as follows, where the last three equations will be needed later for the uncertainty computation.
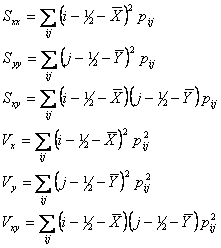 |
(Eq. 2) |
The second moments form a covariance matrix:
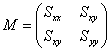 |
(Eq. 3) |
This can be diagonalized to obtain the principal moments and rotation angle as follows.
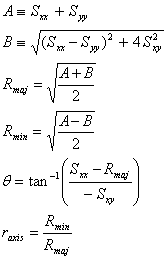 |
(Eq. 4) |
Note that PSFs tend to be well behaved (e.g., not have dominant negative pixels) and not yield cases in which B ≥ A. Such a case would be unphysical and thus have to be rejected; the principal axes must be real and positive definite. The rotation angle here is measured positive right-handed from the X axis of the postage stamp. Rmaj and Rmin are the semimajor and semiminor axes, respectively. The uncertainties are computed as follows, where we assume that the errors are small enough to permit a Taylor series truncated above first order.
 |
(Eq. 5) |
From these we can construct the uncertainties in the axes, angle, and axis ratio:
 |
(Eq. 6) |
Second-moment information is also computed by an alternative method, fitting an elliptical profile to the PSF isophote. The designated isophote is an input parameter that defaults to 10% of the peak. An ellipse is fit to the isophote, deriving the semimajor and semiminor axes, their ratio, and the rotation angle. Another metric that is derived from the PSF is the semimajor axis corresponding to the elliptical fit at the half-power points.