 |
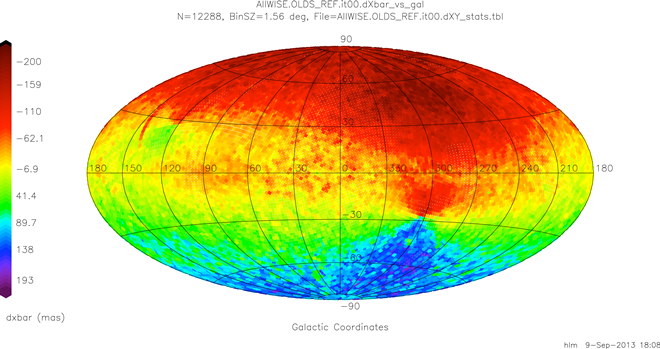
| Figure 1 - Global Bundle-level Mean WISE-2MRef+pm dXu Difference Map at Iteration 0 |



The image coaddition process in the AllWISE Multiframe Pipeline uses the reconstructed position information for each Single-exposure frameset to map images onto the Atlas Tile footprint. Frameset positions were measured by the Single-exposure position reconstruction module (SFPREX) that using a selected subset of the 2MASS catalog (2MRef) as the astrometric reference, without any corrections for the proper motions which occurred between the 2MASS and WISE epochs. Each frameset was reconstructed separately without using information from overlapping frames. Consequently, astrometry of sources in the earlier data releases exhibits a small systematic bias with respect to the ICRS that is the imprint of the motion towards the solar apex. (c.f. All-Sky Release Explanatory Supplement section VI.4.f).
In preparation for AllWISE Multiframe processing, a global refinement of the SFPRex band-frame positions for each input Single-exposure frameset was performed using proper motions from UCAC4 to adjust 2MRef positions while taking into account simultaneously the much larger set of source frame-to-frame position differences in the overlap areas. Because only stars with good quality UCAC4 proper motions are used, the number of reference stars is greatly reduced. However, the use of the large number of stars in the frame-to-frame overlaps compensates by indirectly transmitting reference star inputs from nearby frames.
Schedule and resource limitations did not allow the WCS information in the Single-exposure image headers to be updated with the refined values from the MFPRex processing. However, the refined central positions, rotation angles and pixel scale factors for each frameset used in the AllWISE Multiframe processing is available through the IRSA General Catalog Query Engine. The format of the table of refined Single-exposure WCS information is described in Table 1.
The MFPRex module operates on multiple frames corresponding to overlapping coverages of a specified area on the sky. It also uses matched sets of sources and the 2MRef astrometric reference data (this time corrected for proper motions as determined by UCAC4) to refine the registration of the frames relative to each other and to the proper-motion-adjusted reference star positions. It employs an iterative method that minimizes local coordinate-projection distortion by treating overlapping frames as nodes in a linked list while simultaneously considering differences with respect to the reference star positions. Discrepancy analysis of the matched sources is used to derive corrections to each W1 band-frame's RA, Dec, and Twist. The W1 scales as well as all five parameters needed to provide the other band-frame positions are taken from smoothed SFPRex QA results.
Overall, MFPRex provides a global solution, but given that several million frames are involved, computer resource limitations demand that the task be broken down into manageable chunks. Each execution of the program processes a "bundle" of contiguous frames. HealPix was used on an Ecliptic system with NSIDE=32 to select 12288 roughly equally spaced bundle centers. Given that the entire sky covers approximately 41253 sq-deg, on average each bundle covers 3.36 sq-deg.
Every frame to be processed belongs to one and only one (the closest) bundle. MFPRex is executed separately for each bundle of each iteration. With each iteration, MFPRex steps through all frames belonging to the bundle being processed, treating each frame in turn as the "primary". For each frame, a U-System Cartesian coordinate system is defined to have it's origin at the a priori W1 band-frame center position of the primary. Source positions for all overlapping ("secondary") W1 band-frames are mapped into this coordinate system, and position differences between primary and secondary sources are computed. Reference star positions are also mapped into the primary U-System and primary-reference position differences are computed. A potential full-step adjustment for the primary frame is computed from a combination of primary-secondary and primary-reference differences. The routine stores the full-step adjustments for the primary frame and then proceeds to make the next frame "primary" and the process is repeated.
The U-System is redefined with each new primary frame in order to contain the extent over which a Cartesian system is used to represent what's actually happening on a sphere. Working locally in Cartesian coordinates simplifies and speeds the computations. When the frame already processed shows up later during the iteration as a secondary, the adjustments computed for it are not applied at that point. Frame adjustments computed during one iteration will be applied only on the next iteration. Thus the results are not affected by the order in which the frames are processed.
In order to allow adjustment information to pass between bundles, frames from adjacent bundles are incorporated into the processing. We'll refer to these as "edge" frames as opposed to the "core" frames which actually belong to the bundle being processed. This is another reason frame adjustments are not applied until the next iteration. Information is passed from the previous iteration via disk files. This allows each bundle to be processed independently of all other bundles in that iteration. It doesn't matter what order they are processed in or whether there is a considerable time gap between processing some bundles. The only requirement is that one iteration be complete before moving on to the next. It means that bundles within the same iteration can be run in parallel on different processors. It also provides flexibility to suspend MFPRex processing on all or any subset of processors being used in order to accommodate any higher priority non-MFPRex tasks which may come along. Both are very useful capabilities to have for a long-running high-resource-usage task.
In order to compute the full-step corrections for a primary frame, 3-parameter inverse-variance least-squares fits were made separately for the primary-secondary differences and primary-reference differences. These results were combined to obtain the full-step correction for each frame on each iteration.
At the close of MFPRex processing of an iteration, updated W1 band-frame positions and rotation angles were available. Smoothed band-to-band data previously generated during single-frame pipeline processing via special SFPRex fits made for quality assurance were then used to obtain the other three sets of band-frame positions and rotation angles. Smoothed data from these fits were also used to adjust the X and Y scales of all four bands. See section V.3.c.i for more details.
The initial band-frame positions for MFPRex were just the SFPRex positions determined during single-frame pipeline processing. Given that the SFPRex reconstruction was done w.r.t. 2MRef directly no accounting was made for systematic proper motions of the reference stars during the interval between the 2MASS and WISE epochs. For AllWISE it was decided to include the effects of those proper motions. As a result, the frames initially had relatively large errors w.r.t. the proper-motion-corrected reference stars, as can be seen in figures 1 and 2, which plot mean dXu and dYu differences w.r.t. the proper-motion-corrected reference stats as a function of position on the sky in galactic coordinates. Galactic coordinates were chosen because of the symmetries about the galactic plane which will be seen after 38 iterations in section V-2-b-iv. The dXu and dYu values are in Cartesian coordinates equivalent to local -dRA (true angle) and +dDEC differences, respectively.
 |
| Figure 1 - Global Bundle-level Mean WISE-2MRef+pm dXu Difference Map at Iteration 0 |
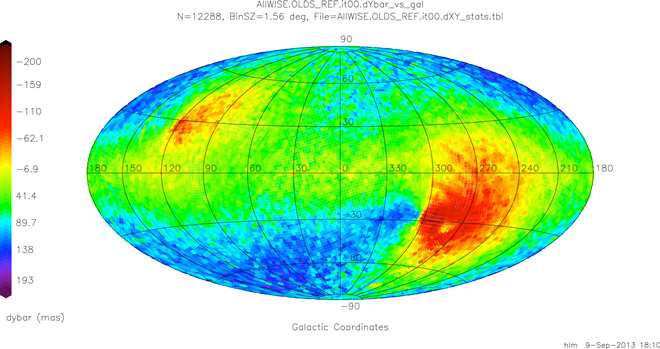 |
| Figure 2 - Global Bundle-level Mean WISE-2MRef+pm dYu Difference Map at Iteration 0 |
The frame-to-frame overlap differences are in much better shape at the initial point. Given that the mean values for the overlap differences will always be zero, mean values of the absolute differences are instead plotted globally in figures 3 and 4.
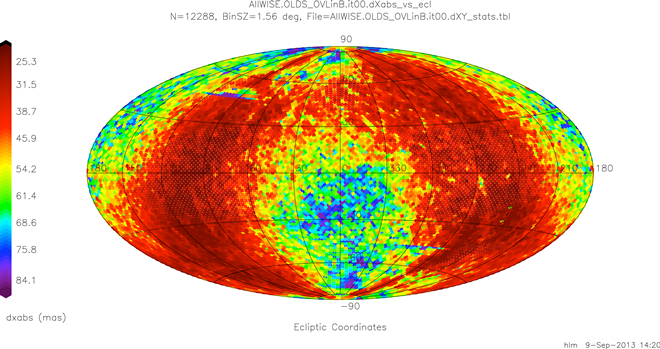 |
| Figure 3 - Global Bundle-level Mean Abs(dXu) Overlap Difference Map at Iteration 0 |
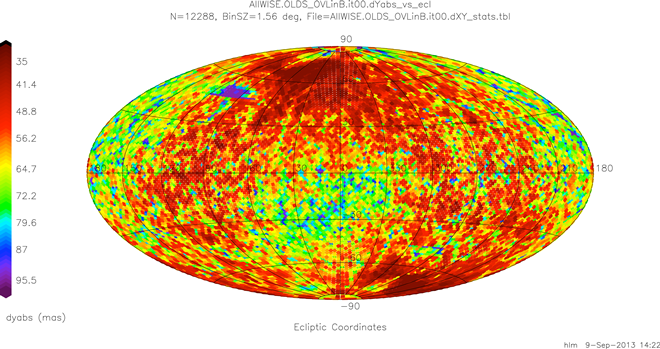 |
| Figure 4 - Global Bundle-level Mean Abs(dYu) Overlap Difference Map at Iteration 0 |
In this case ecliptic coordinates were chosen since the dominant features are the torque-rod scars. These can be seen extending many degrees in ecliptic longitude along constant mid-latitude ecliptic lines in both the north and, less prominently, the south.
V.2.b.iii. Confirmation of convergenceFor a random selection of about 1% of the bundles (n=129) mean absolute values of the dXu, dYu and dTheta step sizes were monitored vs iteration number. These results are presented in figure 5 as a log plot to illustrate that smaller and smaller improvements were being made with increasing iterations. The dXu and dYu means fall almost on top of each other. Rotation follows a similar convergence path but is separated by two orders of magnitude. It takes many milli-aseconds rotation to have a significant effect.
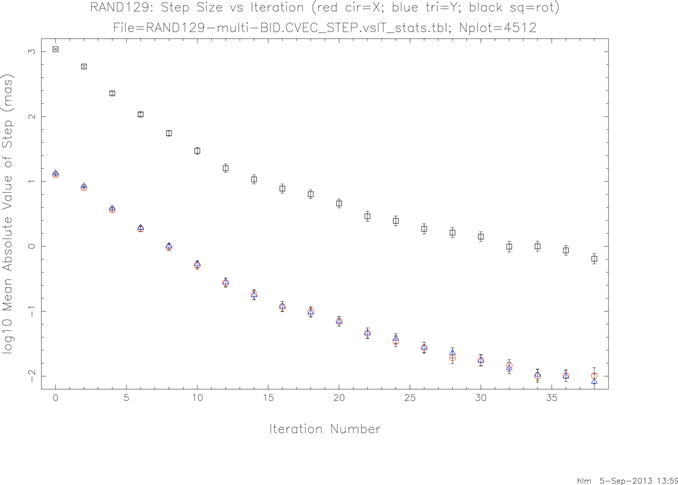 |
| Figure 5 - Log Plot of Mean Absolute Value of Step Size vs Iteration Number |
Looking at it a different way, figure 6 plots the mean magnitude of the remaining dXu position differences vs iteration (blue=overlap & red=ref).
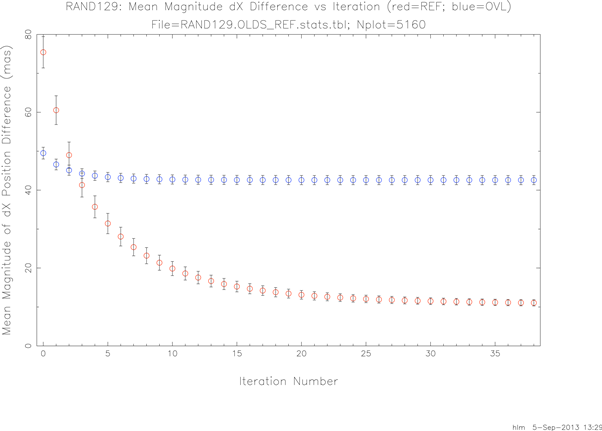 |
| Figure 6 - Mean Abs(dXu) [w.r.t. 2MRef+pm and Overlap Frames] vs Iteration Number |
After 38 iterations there are still some gains being made w.r.t. the reference stars. After the first few iterations the improvement in the overlap differences is almost but not quite leveled out.
Figure 7 shows a very similar pattern for dYu.
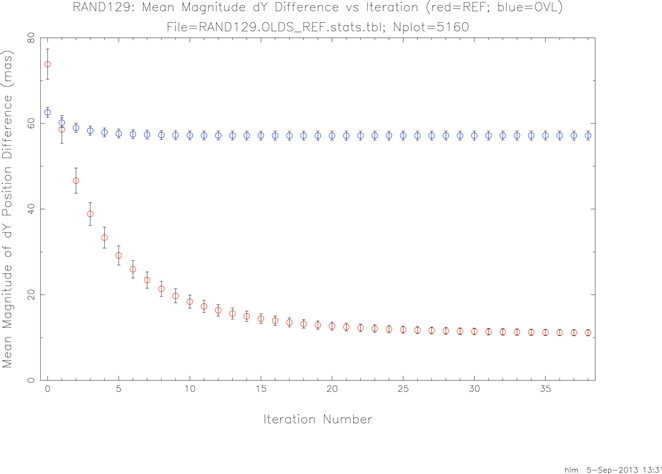 |
| Figure 7 - Mean Abs(dYu) [w.r.t. 2MRef+pm and Overlap Frames] vs Iteration Number |
After 38 iterations most of the original systematic errors w.r.t. the proper motion corrected reference stars have been removed. Figure 8 histograms bundle-level mean differences in dXu after iteration 38 in red, with the initial differences plotted in blue for comparison.
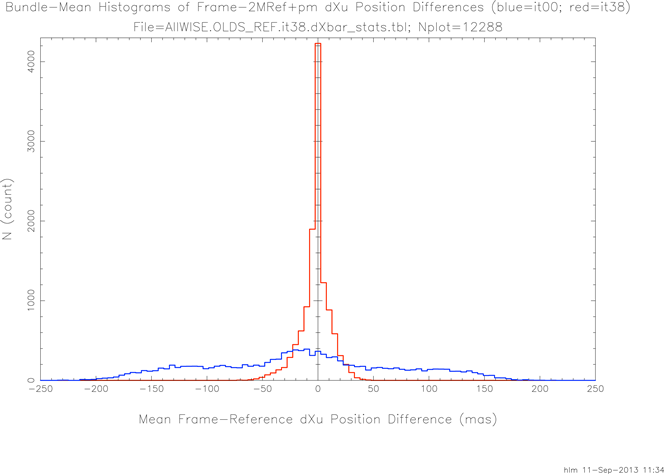 |
| Figure 8 - Bundle-level WISE-2MRef+pm dXu Difference Histograms for Iterations 0 and 38 |
Figure 9 repeats for the dYu values. Once more the improvement is striking but the iteration 38 dYu differences have more bias remaining than for dXu.
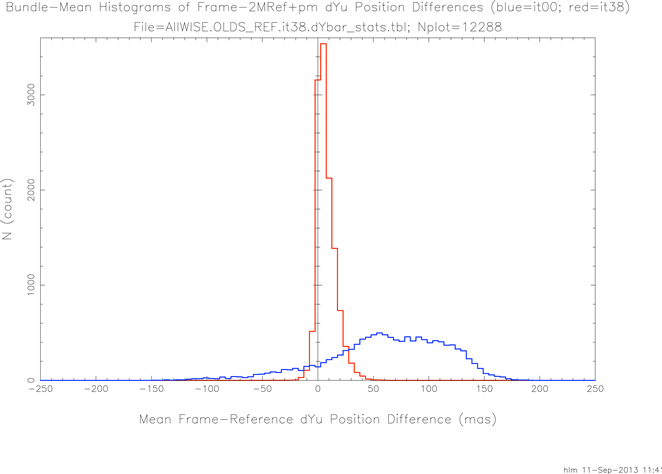 |
| Figure 9 - Bundle-level WISE-2MRef+pm dYu Difference Histograms for Iterations 0 and 38 |
Figure 10 plots frame-level overlap dXu histograms for iteration 38 in red with the initial differences in blue. There is improvement albeit small.
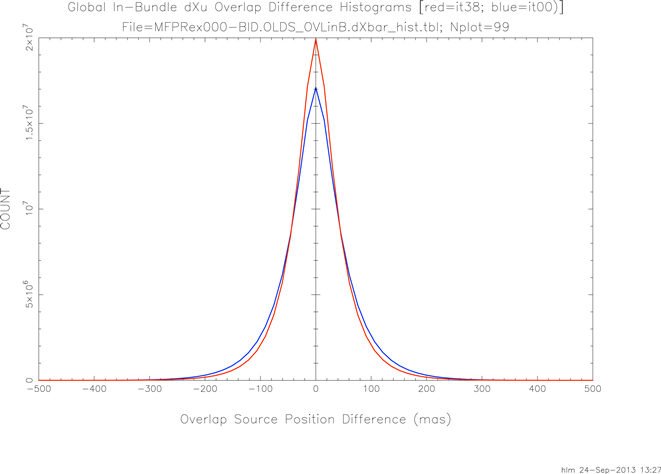 |
| Figure 10 - Frame-level dXu Overlap Difference Histograms at Iterations 0 and 38 |
The same is true for the dYu overlaps as can be seen in figure 11.
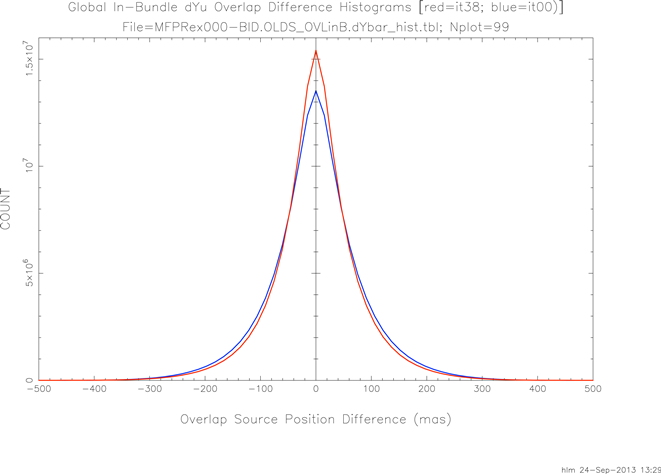 |
| Figure 11 - Frame-level dYu Overlap Difference Histograms at Iterations 0 and 38 |
Mean dXu values w.r.t proper motion corrected reference stars after iteration 38 are plotted globally in galactic coordinates in figure 12.
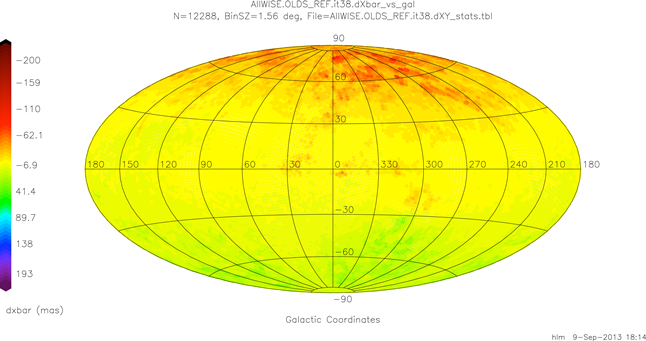 |
| Figure 12 - Global Bundle-level Mean WISE-2MRef+pm dXu Difference Map at Iteration 38 |
This is plotted using the same color scale as the corresponding iteration 0 plot (figure 1) in section V.2.b.ii. It's interesting to note that remaining residual errors increase as you move away from the galactic plane, more or less symmetrically, with opposite signs in the north and south. Figure 13 repeats for dYu which should be compared to figure 2.
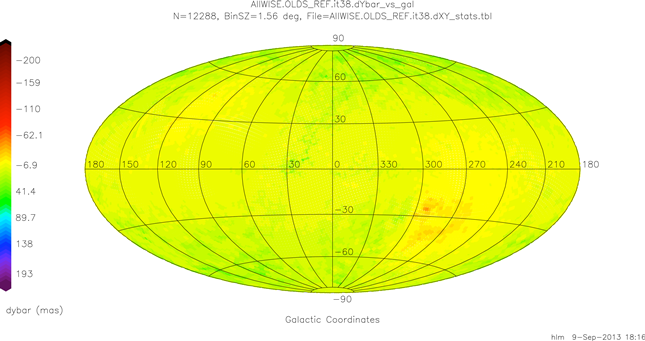 |
| Figure 13 - Global Bundle-level Mean WISE-2MRef+pm dYu Difference Map at Iteration 38 |
Once more there's symmetry about the galactic plane but the signs are the same in the north and south.
Figure 14 plots global iteration 38 absolute value dXu means in ecliptic coordinates.
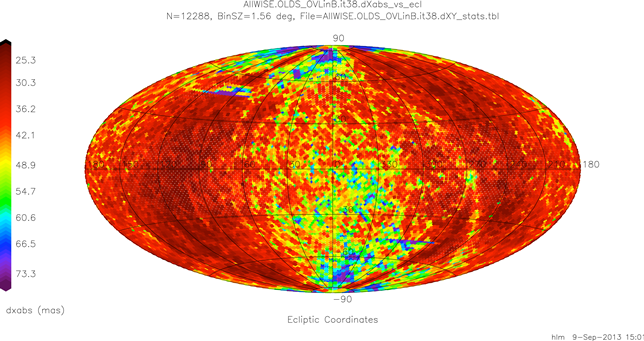 |
| Figure 14 - Global Bundle-level Mean Abs(dXu) Overlap Difference Map at Iteration 38 |
The differences w.r.t. the iteration 0 plot (figure 3) are insignificant. Figure 15 repeats for dYu with o apparent changes from the corresponding iteration 0 plot (figure 4).
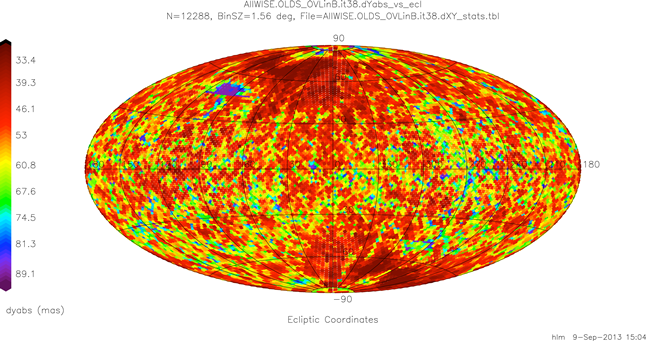 |
| Figure 15 - Global Bundle-level Mean Abs(dYu) Overlap Difference Map at Iteration 38 |
By the time iteration 38 was complete there was little schedule time left for further iterations, despite the fact that some improvement w.r.t. proper-motion-corrected reference stars was occurring with each iteration.
At this point removing the remaining mean reference star residuals at the bundle level was considered. Note that this is quite different from removing the reference star residuals at the frame level. By doing the final adjustment at the bundle level, the frame overlap differences for the hundreds of frames within each bundle are preserved. The question remaining is how much damage is done to the cross-bundle frame overlaps. Figure 16 presents dRA (red) and dDEC (blue) histograms of the relative bundle-to-bundle shifts introduced.
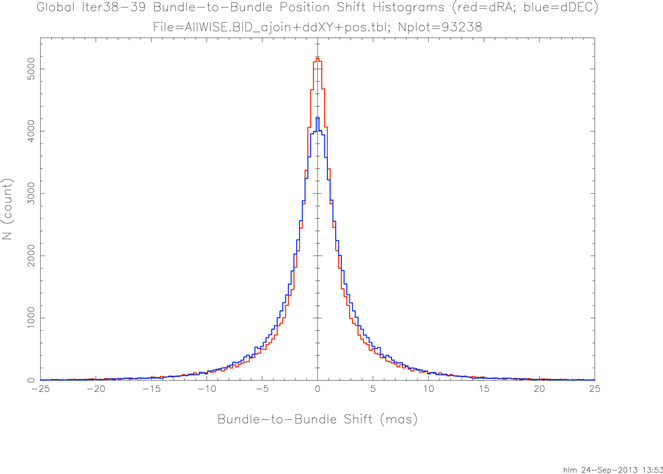 |
| Figure 16 - Histograms of Relative Bundle-to-Bundle Shifts Introduced |
Given that the vast majority of the additional cross-bundle frame-to-frame differences induced were well below 10 mas, the decision was made to do a bundle-level reference bias removal between iteration 38 and 39. The band-frame parameters from iteration 39 were used for AllWISE processing.
Last update: 27 March 2019